ESTA PROPOSTA DE ATIVIDADE DE MATEMÁTICA É DESTINADA AOS ESTUDANTES DO 4º ANO DO ENSINO FUNDAMENTAL.
Calculando áreas na malha quadriculada
A malha quadriculada é formada por pequenos quadrados. Cada quadrado tem um lado igual ao comprimento de um quadradinho.

Nesta malha temos: cada quadradinho tem 1 cm de largura e 1 cm de comprimento. Formando assim uma área de 1 cm2 (lemos: um centímetro quadrado).
Quando calculamos a área de uma figura, estamos medindo quanto espaço ela ocupa em uma superfície plana, como uma folha de papel. A área é sempre expressa em unidades quadradas, porque estamos medindo a quantidade de quadrados que cabem dentro dessa figura.
Para calcular a área de uma figura na malha quadriculada, você precisa contar quantos quadradinhos estão completamente dentro da figura.
Por exemplo:
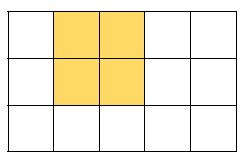
O quadrado amarelo está ocupando 4 quadradinhos inteiros, então a área desse quadrado é 4 cm2 (quatro centímetros quadrados).
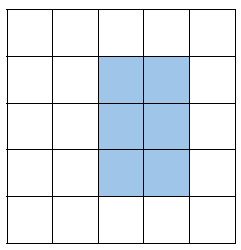
O retângulo está ocupando 6 quadradinhos inteiros, então sua área é 6 cm2 (seis centímetros quadrados).
QUESTÃO 1
Observe o desenho na malha quadriculada:

Qual área ele ocupa?
a) 60
b) 63
c) 65
d) 70
QUESTÃO 2
Pedro escreveu a palavra ‘área’ na malha quadriculada:

Quanto de área da malha quadriculada ele ocupou ao escrever esta palavra?
a) 46
b) 48
c) 50
d) 52
QUESTÃO 3
Imagine que você tem um desenho de uma sala na malha quadriculada, com 5 quadradinhos de largura e 4 quadradinhos de altura. Como você calcularia a área dessa sala? Explique passo a passo o processo de cálculo. Se desejar, desenhe na malha quadriculada para facilitar a visualização.
QUESTÃO 4
Suponha que você tenha uma figura irregular (com lados diferentes) desenhada em uma malha quadriculada. Como você calcularia a área dessa figura? Descreva os passos que você seguiria para determinar a área corretamente, utilizando a contagem dos quadrados da malha como referência. Dê um exemplo prático para demonstrar como resolver essa situação.
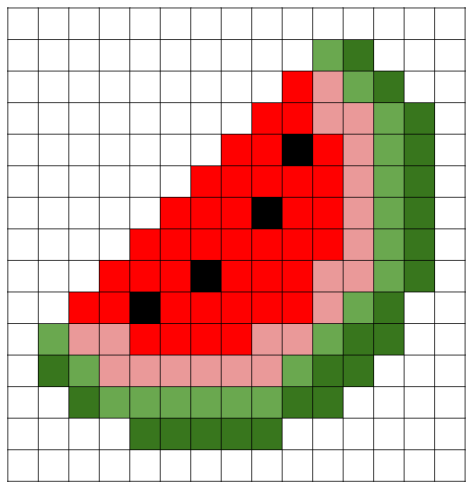
Veja um exemplo de figura irregular:

| Autoria: | Lucyana Oliveira Borba |
| Formação: | Pedagogia |
| Componente Curricular: | Matemática |
| Habilidades: | (EF04MA21-A) Estimar área de figuras planas desenhadas em malha quadriculada, pela contagem dos quadradinhos ou de metades de quadradinho, reconhecendo que duas figuras com formatos diferentes podem ter a mesma medida de área. (EF04MA21-B) Medir e comparar área de figuras planas desenhadas em malha quadriculada, pela contagem dos quadradinhos ou de metades de quadradinho, reconhecendo que duas figuras com formatos diferentes podem ter a mesma medida de área. |
| Referências: | BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2018. CADERNO APRENDER SEMPRE – 2º Bimestre 2023- 4º Ano/ Ensino Fundamental/ Língua Portuguesa e Matemática/ Prefeitura de Goiânia- Secretaria Municipal de Educação. Documento Curricular para Goiás (DC-GO). Goiânia/GO: CONSED/ UNDIME Goiás, 2018. Disponível em: <https://cutt.ly/MOsX7AS> acessado em 26, jan. 22. |