Esta atividade de Matemática tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 7º ano do Ensino Fundamental.
Construção
Podemos usar régua e compasso para fazer diversos desenhos. Para desenhar um triângulo conhecendo as medidas de seus lados e usando somente uma régua é muito complicado. Então essas ferramentas simples nos permitem construir triângulos com bastante precisão. Veja como realizar essa construção:
1°) Devemos definir o comprimento de um dos lados do triângulo.
2°) Usando a régua vamos traçar uma linha para representar esse lado. Lembrando que os pontos extremos dessa linha serão vértices do triângulo.
3°) Usando a régua vamos ajustar o compasso com a medida de um dos outros lados.
4°) Com uma ponta do compasso no vértice marcado, traçamos um arco acima da linha reta.
5°) Ajuste o compasso com a medida do terceiro lado.
6°) Com uma ponta do compasso no outro vértice marcado, traçamos um arco cruzando o primeiro arco construído.
7°) A intersecção desses arcos será o terceiro vértice do triângulo.
8°) Faça os outros lados do triângulo unindo os vértices.
Retas paralelas intersectadas por uma transversal
Duas retas são consideradas paralelas, quando elas não tem nenhum ponto em comum. Ou seja, quando elas mantêm a mesma distância uma da outra ao longo de toda a sua extensão. Podemos pensar em retas paralelas como as hastes coloridas da cerca nessa imagem:

Disponível em: <Área De Brincar Parque Infantil – Foto gratuita no Pixabay – Pixabay> Último acesso em 06 de maio de 2023.
Uma reta transversal intersecta uma ou mais retas. Quando retas paralelas são intersectadas por uma transversal, diversas relações surgem entre os segmentos de reta e os ângulos formados.

Disponível em: <Cerca De Jardim Madeira – Foto gratuita no Pixabay – Pixabay> Último acesso em 06 de maio de 2023.
Ao traçarmos duas retas paralelas (r // s) e também uma reta transversal t que intercepta r e s, formaremos oito ângulos. Esses ângulos podem ser classificados de acordo com a sua posição:

Imagem do arquivo pessoal
- Os ângulos que estão entre as retas paralelas são internos e os demais ângulos são externos.
- Se dois ângulos estão à direita ou à esquerda da transversal dizemos que são colaterais. Mas se estão em lados alternados dizemos que são alternos.
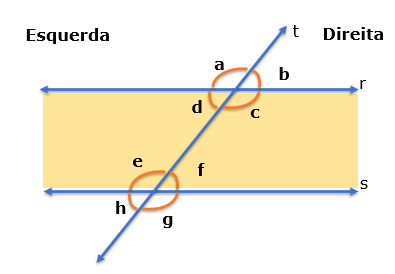
Imagem do arquivo pessoal
Os ângulos que estão em posições correspondentes em relação à transversal (alternos internos e alternos externos são congruentes, ou seja, tem a mesma medida. Os ângulos formados pelos lados opostos da intersecção são opostos pelo vértice e também são congruentes. Então:
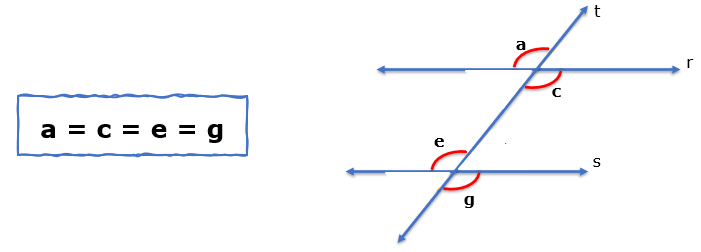
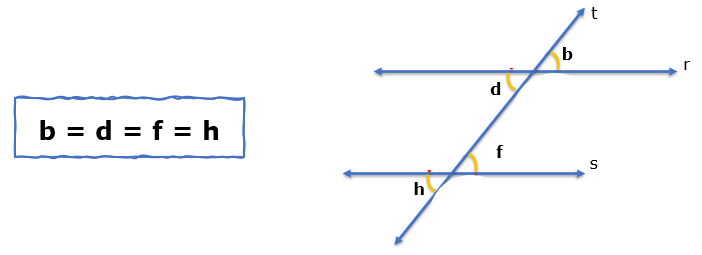
Imagem do arquivo pessoal
Quando uma transversal intersecta duas retas paralelas, ângulos suplementares também podem ser encontrados. Dois ângulos são suplementares quando a soma de suas medidas é igual a 180 graus. Os ângulos suplementares são encontrados nos pares formados por um ângulo interno e um ângulo externo na mesma posição em relação à transversal.
De acordo com a imagem podemos concluir que:
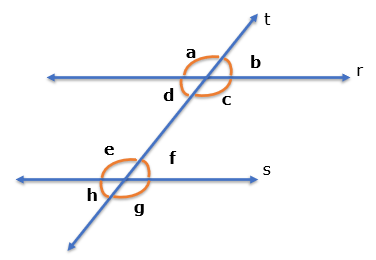
Imagem do arquivo pessoal
| a + b = 180° | e + f = 180° | a + f = 180° | d + e = 180° |
| b + c = 180° | f + g = 180° | a + h = 180° | d + g = 180° |
| c + d = 180° | g + h = 180° | b + e = 180° | c + f = 180° |
| d + a = 180° | h + e = 180° | b + g = 180° | c + h = 180° |
Essas são apenas algumas das propriedades e relações que podem ser observadas quando retas paralelas são intersectadas por uma transversal. Esses conceitos são fundamentais na geometria e são aplicados em várias áreas, como arquitetura, engenharia, física e design.
Assista a videoaula com a professora Priscilla com essa temática
Agora que você estudou sobre construção de triângulos e relação entre alguns ângulos, vamos responder algumas questões?
Questão 1
Alice quer fazer um trabalho escolar sobre triângulos escalenos e precisa desenhar numa cartolina um triângulo cujos lados medem 10 cm, 8 cm e 6 cm. Usando régua e compasso faça o desenho desse triângulo.
Questão 2
A figura a seguir mostra duas retas paralelas interceptadas por uma transversal. Calcule os valores dos ângulos b, c, d, e, f, g e h.
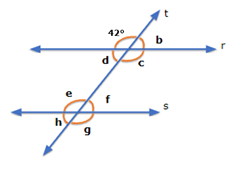
Imagem do arquivo pessoal
Questão 3
Um parque tem uma área de lazer com dois conjuntos de barras paralelas, usadas para exercícios de ginástica. Um trampolim foi colocado perpendicularmente aos conjuntos de barras, intersectando ambos. Nesta situação, podem ser encontrados
(A) 2 pares de ângulos suplementares.
(B) 3 pares de ângulos suplementares.
(C) 4 pares de ângulos suplementares.
(D) 6 pares de ângulos suplementares.
Questão 4
Em uma cidade, duas avenidas, A e B, foram construídas paralelamente uma à outra. Um novo cruzamento foi planejado, e uma terceira avenida, C, foi construída cruzando perpendicularmente as duas avenidas paralelas, A e B.
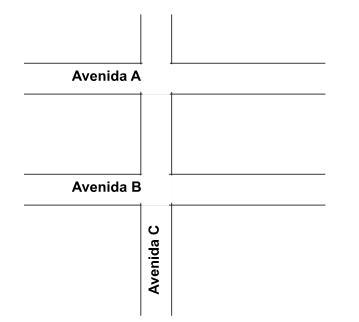
Fonte: Acervo NEC – produzido no Google Desenhos.
Após a construção da Avenida C,
(A) as duas avenidas paralelas, A e B, agora são perpendiculares entre si.
(B) as duas avenidas paralelas, A e B, permanecem paralelas.
(C) esta se tornou paralela a uma das avenidas, A ou B.
(D) as duas avenidas paralelas, A e B, se tornam concorrentes entre si.
| Autoria: | Priscilla Nascimento Dias, licenciada em Matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA25-A) Reconhecer a abertura do ângulo como grandeza associada às figuras geométricas e reconhecer os diferentes tipos de ângulos: agudo, reto e obtuso. (EF06MA25-B) Associar mudanças de direção e giros em trajetos em malhas quadriculadas e da leitura de mapas à noção e uso do ângulo em situações diversas. (EF06MA26-A) Reconhecer e comparar ângulos. (EF06MA26-B) Identificar ângulos: nulo, reto, raso, meia volta e de uma volta. (EF06MA26-C) Resolver problemas que envolvam a noção de ângulo em diferentes contextos e em situações reais, como ângulo de visão. (EF07MA24-A) Construir triângulos, usando régua e compasso. (EF07MA24-B) Reconhecer a condição de existência do triângulo quanto à medida dos lados. (EF07MA24-C) Verificar que a soma das medidas dos ângulos internos de um triângulo é 180° e aplicar este resultado para demonstrar o teorema do Ângulo Externo. (EF07MA23-A) Explorar as relações entre os ângulos formados por retas paralelas cortadas por uma transversal, através de atividades experimentais com dobraduras e materiais manipuláveis. (EF07MA23-B) Identificar pares de ângulos consecutivos, adjacentes, caso particular dos ângulos consecutivos, colaterais internos e externos, alternos internos e externos, correspondentes e opostos pelo vértice. (EF07MA23-C) Verificar relações entre os ângulos formados por retas paralelas cortadas por uma transversal, com e sem uso de softwares de geometria dinâmica, para a utilização em situações problema diversas. |
