Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 6º Ano do Ensino Fundamental – Anos Finais.
Ampliação e redução de polígonos na malha quadriculada
Você já percebeu como algumas imagens podem ser aumentadas ou diminuídas sem perder a forma? Isso acontece, por exemplo, com mapas e fotografias. Um mapa é uma representação reduzida de um lugar real, onde todas as medidas são diminuídas de maneira proporcional para criar uma cópia menor, mas fiel à original.
Na Geometria, podemos explorar esses conceitos usando a malha quadriculada para ampliar ou reduzir figuras planas, como polígonos. Esse processo se chama homotetia, que é uma transformação geométrica que altera o tamanho da figura sem mudar sua forma, mantendo a proporção entre os lados e a igualdade dos ângulos.
A malha quadriculada é um recurso que auxilia na representação de figuras planas. Cada quadradinho da malha é uma unidade de medida, que pode ser em cm (centímetro), m (metro) ou outra.
Homotetia de Polígonos na Malha Quadriculada
Quando aplicamos a homotetia, a nova figura é semelhante à original, ou seja, tem a mesma forma, os mesmos ângulos e lados proporcionais. Para ampliar uma figura, multiplicamos todos os seus lados por um número chamado fator de ampliação. Por exemplo, se quisermos dobrar o tamanho de um triângulo como na imagem a seguir, multiplicamos o comprimento de cada lado por 2.
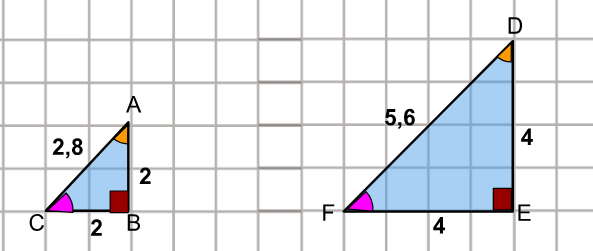
FONTE: Acervo NEC – produzido no canva.com.
No caso da redução, o processo é parecido: multiplicamos os lados por um fator menor que 1. Se quisermos reduzir a figura à metade do tamanho original, multiplicamos cada lado por 0,5 (ou ½).
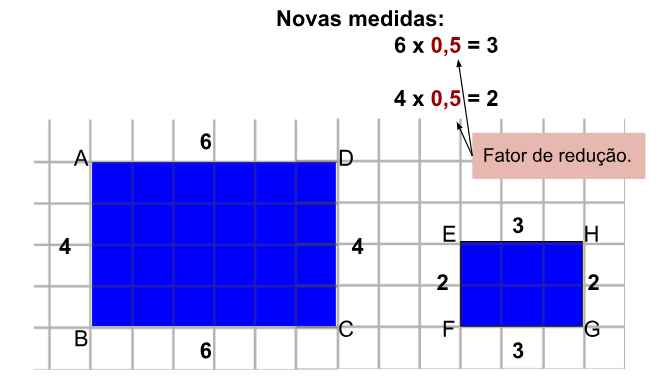
FONTE: Acervo NEC – produzido no canva.com
Para calcular o fator de ampliação ou de redução, basta dividir quaisquer dois lados correspondentes da figura. Na imagem acima, como se trata de uma redução, vamos dividir o menor pelo maior.
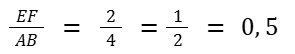
Proporcionalidade em Lados, Perímetro e Área
Quando ampliamos ou reduzimos uma figura, não são apenas os lados que mudam. O perímetro e a área também sofrem alterações proporcionais:
- Lados: São multiplicados diretamente pelo fator de ampliação ou redução.
- Perímetro: Como o perímetro é a soma dos comprimentos dos lados, ele também é multiplicado pelo mesmo fator.
- Área: A área muda de forma diferente. Se o fator de ampliação for 2, a área aumentará em 2² = 4 vezes. Se o fator de redução for 0,5, a área diminuirá em (0,5)² = 0,25, ou seja, será ¼ da original.
Veja esse exemplo:
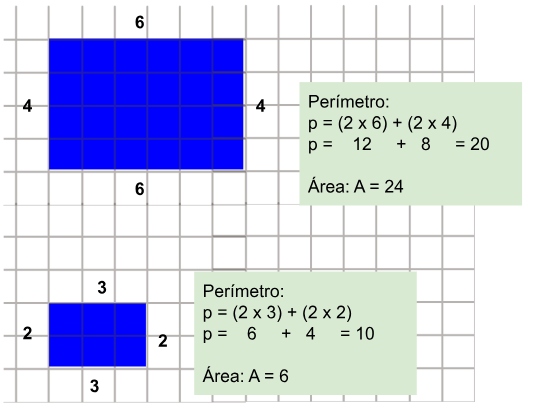
FONTE: Acervo NEC – produzido no canva.com
Esses conceitos da proporcionalidade na ampliação e redução de imagens são importantes e aplicáveis em diferentes áreas como Arquitetura, Design, Cartografia, entre outras.
Para compreender melhor os conceitos apresentados aqui, assista ao vídeo “Ampliação, redução e proporcionalidade”, da professora Cristiane Souza, do canal YouTube, Estúdio Conexão Escola.
Agora, resolva a estas questões.
QUESTÃO 1
Observe os trapézios representados na imagem a seguir.
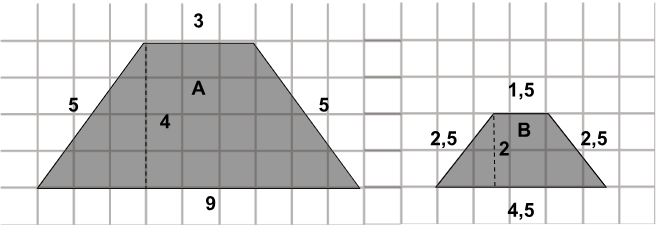
Comparando esses polígonos
(A) A é uma redução de B.
(B) A é igual a B.
(C) B é uma redução de A.
(D) B é uma ampliação de A.
QUESTÃO 2
O triângulo ABC e DEF são semelhantes, sendo DEF uma ampliação de ABC.
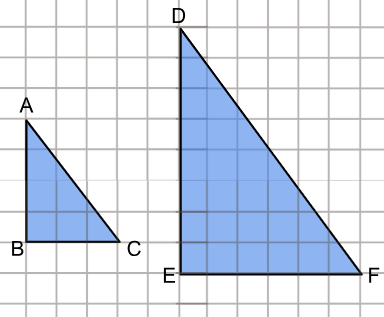
O fator de ampliação usado na transformação de ABC para DEF é
(A) 2.
(B) 4.
(C) 0,5.
(D) ⅓.
QUESTÃO 3
Piet Mondrian foi um pintor holandês modernista, conhecido por utilizar em suas obras, formas geométricas simples como o quadrado e o retângulo e pelo uso das cores primárias (vermelho, azul e amarelo), além do preto, branco e cinza. Suas pinturas destacam a harmonia entre formas e cores, criando composições marcantes.
A moldura a seguir é inspirada no estilo Mondrian e está representada numa malha quadriculada.
Calcule:
A) O perímetro da moldura.
B) Se os lados dessa moldura for ampliada com fator 3, qual será o novo perímetro?
C) Qual é a área ocupada pela moldura?
QUESTÃO 4
A logomarca da empresa de Magda está representada na malha quadriculada abaixo.
Essa logomarca será ampliada em 3 vezes para ser impressa em um cartaz. Comparando com a original,
A) quanto aumentará no perímetro da logomarca após a ampliação?
B) qual é a medida da área do cartaz ocupada pela logomarca?
QUESTÃO 5
O polígono abaixo é um paralelogramo. Amplie este polígono usando a malha quadriculada.
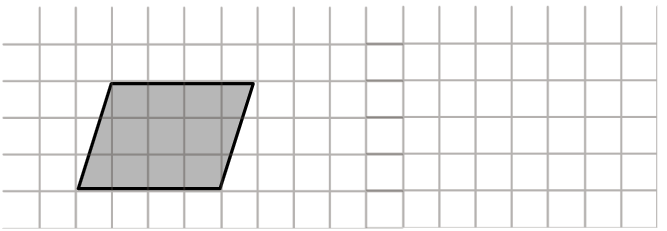
Qual será a área do paralelogramo após a ampliação?
| Autoria: | Cristiane Soares de Souza |
| Formação: | Matemática – Licenciatura |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA21) Construir figuras planas semelhantes em situações de ampliação e de redução, com o uso de malhas quadriculadas, plano cartesiano ou tecnologias digitais. |
| Objetos de conhecimento: | Ampliação e redução de polígonos usando a malha quadriculada; cálculo de perímetro e área de polígonos na malha quadriculada; ideia de proporcionalidade; semelhança de polígonos. |
| Referência: | SILVEIRA, Ênio. Matemática: compreensão e prática. 5ª edição, São Paulo, Moderna, 2018. PEREIRA, Marcos Fabrício Ferreira. Uma Sequência Didática para o ensino de Semelhança de Figuras Planas. XX Ebrapen – Encontro Brasileiro de Pós-graduação em Educação Matemática, 2016. Disponível em http://www.ebrapem2016.ufpr.br/wp-content/uploads/2016/04/gd2_Marcos_Fabricio.pdf, consultado em 17/03/2025. |
