Olá, educando (a)! Esta videoaula de Matemática para o 9º ano do Ensino Fundamental – foi veiculada na tv no dia 01/04/2021 (quinta-feira). Aqui no portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade, você, estudante do 9º ano, irá identificar e reconhecer os: monômios, binômios, trinômios e polinômios, fazendo a relação entre esses componentes algébricos com as equações do primeiro grau.

Assista a videoaula abaixo, com a temática: Álgebra: uma introdução aos polinômios e equações
Olá, nesta atividade você vai estudar sobre os conceitos algébricos de polinômios e equações polinomiais do primeiro grau. Para iniciar os estudos, veja as explicações sobre os conceitos algébricos dos polinômios.
Um termo algébrico é sempre composto de dois termos principais: coeficiente e parte literal. O coeficiente é o número que acompanha as variáveis e a parte literal são as próprias variáveis.
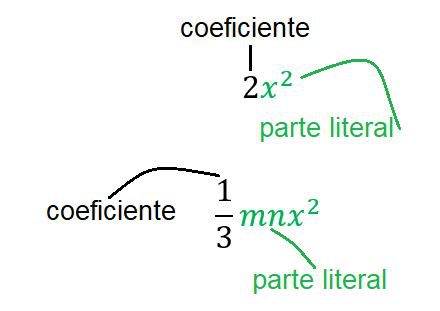
Assim, os polinômios são compostos, por: coeficiente (números que acompanham as variáveis) e parte literal (variáveis – letras que representam números).
Estudo sobre os Polinômios
Para compreender o que são polinômios é necessário traçar um caminho que seja possível conjecturar os polinômios, e, este caminho perpassa alguns conceitos de área e perímetro na geometria. Apesar do conteúdo matemático dos polinômios serem algébricos, eles podem ser percebidos no contexto da geometria.
Observe:

Agora analise a situação abaixo:
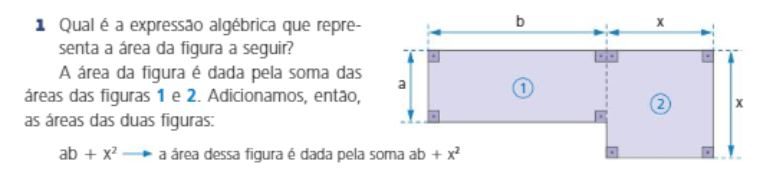
Na composição das duas figuras (figura 1 e figura 2), tem-se um binômio, pois representa a soma de dois termos algébricos.
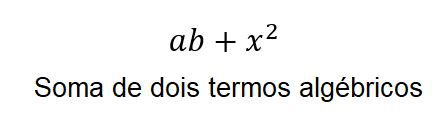
Assim, você já deve ter percebido que a classificação dos polinômios, podem ser representada por monômios, binômios, trinômios e polinômios.
No esquema abaixo, verifica-se essa classificação:
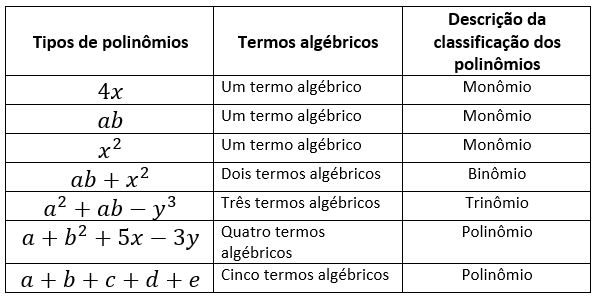
Como você percebeu no esquema:
- Os monômios apresentam somente um único termo algébrico (não há soma nem subtração);
- Os binômios apresentam a soma ou subtração de dois termos algébricos;
- Os trinômios apresentam a soma ou subtração de três termos algébricos;
- Os polinômios apresentam a soma ou subtração de quatro ou mais termos algébricos.
Agora, veja uma situação onde é possível agrupar termos algébricos semelhantes:
Na imagem abaixo, tem-se a composição de cinco figuras, que juntas formam um todo. Procure calcular a área de cada uma das figuras que compõe toda a imagem e depois dê a área total da figura:
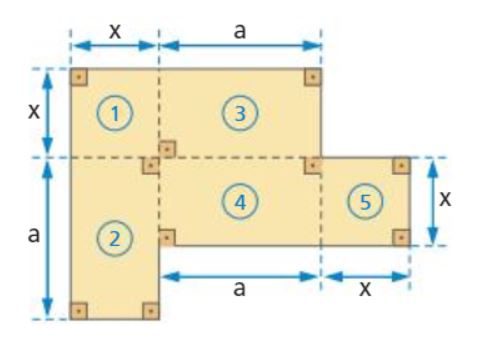
Para solucionar esse problema, tem-se que realizar o cálculo da área de cada uma das figuras que compõe toda a imagem, como mostra, abaixo:

Pode-se concluir que os polinômios que possuem termos semelhantes, podem ser agrupados em um único termo, e, que nesta situação, tem-se como resultado final um binômio que representa a área total, pois está representado pela soma de dois termos.
O estudo dos polinômios possibilita a definição de outro conceito algébrico, que é o conceito de equação. No próximo tópico, você estudará sobre as equações e as suas possíveis relações com os polinômios.
Equações polinomiais do 1º grau
As equações polinomiais do 1º grau, como o próprio nome sugere, são polinômios que estão em igualdade com outros polinômios, pois a palavra equação indica igualdade e faz-se necessário o uso desse sinal matemático, para representá-la.
Para compreendermos de fato o que é uma equação, utiliza-se o exemplo abaixo, que perpassa um instrumento antigo, utilizado por nossos antepassados recentes, que é a balança de dois pratos. Na balança de dois pratos, os pesos devem ser iguais em cada um dos pratos pra que ela esteja em equilíbrio. No caso de nosso exemplo, a balança está em equilíbrio, pois mantém o mesmo peso em cada um de seus pratos.
Agora observe com muita atenção este exemplo:
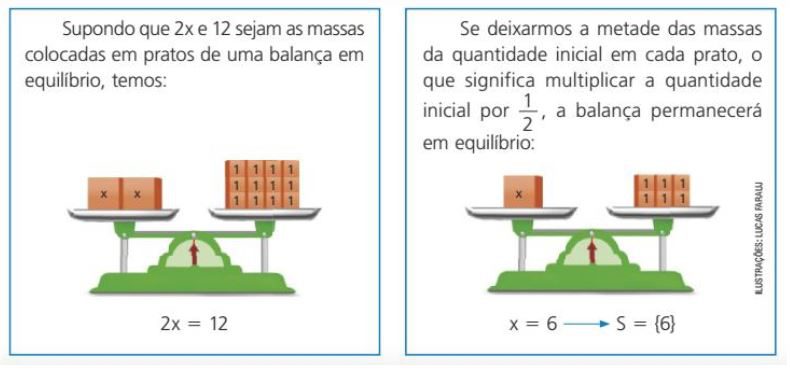
No exemplo, tinha-se do lado direito da balança duas peças, cada uma valendo x, ao total de 2x e no outro prato tínhamos doze peças, cada uma com o símbolo de um peso. Desse modo, tínhamos a equação:
2x = 12
Esta equação, foi modificada, retirando a metade dos pesos do prato direito e metade dos pesos do prato esquerdo, o que ocasionou:
x = 6
Ao fazer esse movimento na balança, descobrimos quanto pesava a peça x que estava do lado direito, ressaltando que para cada peça x de um lado, eram necessárias 6 peças do outro lado para que elas mantivessem o equilíbrio. Aqui, tem-se um exemplo clássico do que é uma equação e a forma como procedemos para resolver e determinar um valor desconhecido (incógnita) de uma equação.
Para que você possa se familiarizar com o conceito de equação, observe o outro exemplo:
Na imagem abaixo, considere que cada uma das maçãs tenha exatamente o mesmo peso que as outras.

Se chamarmos cada uma das maçãs de x, tem-se uma equação:
Do lado direito, os pesos serão representados por: 2x + 400g;
Do lado esquerdo, os pesos serão representados por: 4x + 200g.
Logo, a equação será:
2x + 400 = 4x + 200
Retirando de cada um dos lados duas maçãs (2x) e um peso de 200g, a equação ficará:
200 = 2x
Restando: do lado direito somente o peso de 200g e do lado esquerdo 2 maçãs (2x)
Ora, se duas maçãs pesa 200g, logo, cada uma das maçãs irá pesar 100 g,
O valor do peso de cada maçã, será de 100g
100 = x
Resolvendo a equação proposta na balança de dois pratos.
Agora é com você! Resolva as situações problemas abaixo:
Questão 01. Observe com muita atenção a imagem abaixo:
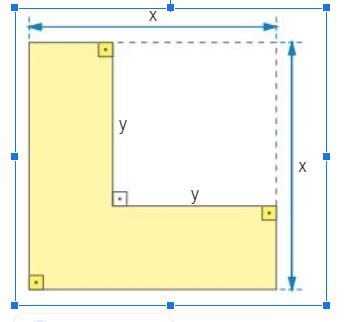
a) Escreva o polinômio que representa a área da região colorida em amarelo da imagem abaixo:
b) Classifique esse polinômio quanto ao número de termos que ele possui:
c) Se x vale 10 cm e y vale 6 cm, qual é o valor da área amarela em centímetros quadrados?
Questão 02. Observe a balança de dois pratos e faça o que se pede:
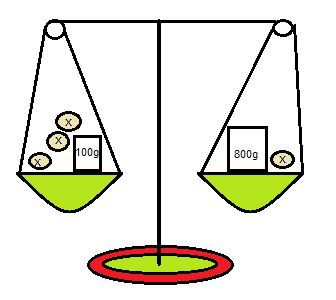
a) Qual é a equação que representa algebricamente o equilíbrio da balança?
b) Resolva a equação e determine qual é o peso de cada uma das bolinhas.
Em síntese, nesta atividade você pôde (re)lembrar alguns conceitos algébricos e geométricos, compreendendo o conceito de polinômio, sabendo classificá-los quanto ao número de termos, e, estudou sobre os conceitos que envolvem equações polinomiais do primeiro grau, resolvendo situações problemas capazes de colocar em prática todo o estudo desenvolvido com a atividade de hoje.
Até a próxima atividade com mais estudos matemáticos.
Bons estudos!
| Habilidades | Habilidades Estruturantes (EF08MA06-D) Associar os polinômios aos modelos geométricos de figuras planas (cálculo de perímetros e áreas), aos modelos de sólidos geométricos (cálculo de áreas da base e áreas laterais em planificações, cálculo de volumes) e os modelos que surgem em diversas situações do cotidiano como o valor a se pagar numa corrida de táxi, os valores de receita, custo e lucro de uma empresa dependendo da quantidade de produtos comercializados, entre outras. (EF09MA06-A) Descrever em contextos práticos as relações de proporcionalidade direta entre duas grandezas por meio de funções de 1° grau. (EF09MA06-B) Ler, interpretar, resolver e elaborar problemas com parte fixa e parte variável que podem ser expressas por funções do 1° grau, calculando valores numéricos e estabelecendo o comportamento da função (crescente ou decrescente) para um determinado intervalo de valores numéricos. Habilidade Complementar EF09MA06-H |

