Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 6º Ano do Ensino Fundamental – Anos Finais.
Operações com frações: adição e subtração
A fração é uma divisão, mas o seu significado está além de dividir dois números. Na verdade, a fração indica “parte de algo que foi dividido”. Por exemplo, ¼ é o mesmo que “1 dividido por 4”. Porém, estamos querendo dizer que: se algo foi dividido em 4 partes, estamos considerando apenas uma dessas partes.

Assim como os números inteiros, as frações também podem ser somadas ou subtraídas. Estas são operações comuns no nosso cotidiano, como ajustar quantidades em receitas, por exemplo.
Para realizar essas operações corretamente, é importante observar os denominadores.
Adição e subtração de frações:
A) Com denominadores iguais
Veja esse exemplo:
- Uma receita indicava ¾ de xícara de farinha de trigo. Como a massa ainda não estava no ponto, a cozinheira acrescentou ¼ de xícara de farinha de trigo. Quanto de farinha a cozinheira usou nessa receita?
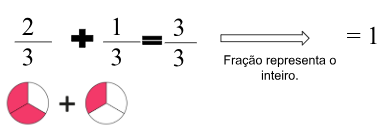
Como os denominadores são iguais, representam divisões na mesma quantidade de partes. Neste caso, repete o denominador e soma ou subtrai os numeradores.
Vamos a outro exemplo, desta vez, subtração.
- Em um galão de tinta, havia ⅝ do total de tinta. Foram gastos ⅜ na pintura do quarto. Quanto de tinta restou ainda?
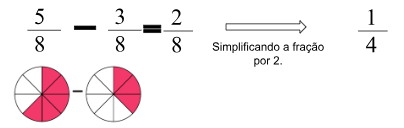
B) Com denominadores diferentes
Para preparar um bolo, são necessários ¾ de xícara de açúcar e ⅔ de xícara de farinha de trigo. Somando esses ingredientes secos, qual é a quantidade total usada na receita?
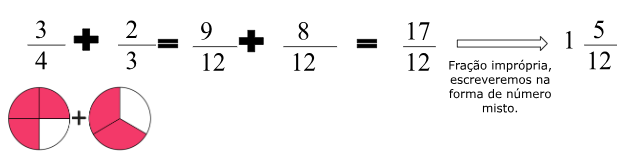
Observe que, neste exemplo, as frações representam partes de tamanhos diferentes. Isso acontece porque os denominadores são diferentes — ou seja, o todo foi dividido em quantidades diferentes de partes.
Para conseguir somá-las ou subtraí-las corretamente, é preciso transformá-las em frações equivalentes com o mesmo denominador (cálculo do mínimo múltiplo comum ou MMC). No exemplo acima, o MMC (3, 4) = 12.
Essas operações fazem parte do nosso dia a dia e nos ajudam a resolver situações reais com mais precisão, como medir, repartir ou ajustar quantidades.
Para reforçar o conceito de fração, assista à videoaula do canal Estúdio Conexão Escola, Frações: conceito e classificações, da professora Cristiane Souza.
Agora, aplique o que você aprendeu resolvendo as atividades a seguir.
QUESTÃO 1
“Na adição ou subtração de frações com denominadores _______________, repete o denominador e, soma ou subtrai os numeradores.”
A palavra que completa corretamente a frase acima é
(A) iguais.
(B) diferentes.
(C) nulos.
(D) ímpares.
QUESTÃO 2
Na fazenda de Antônio,
- ½ da área foi usada para o plantio de milho;
- ¼ da área foi usada para o plantio de trigo.
Agora responda:
A) Qual fração da área da fazenda está ocupada com as duas plantações?
B) Qual fração da área da fazenda não é usada por essas duas plantações?
QUESTÃO 3
Aline fez uma pesquisa com os colegas da sua turma para escolherem a cor da camiseta dos jogos internos da escola. Cada estudante podia escolher no máximo uma das cores, entre roxa e amarela.
Os resultados da pesquisa foram:
- ⅓ da turma escolheu a cor roxa;
- ⅖ da turma escolheu a cor amarela.
Responda:
A) Usando desenhos, represente as frações dos resultados da pesquisa da Aline.
B) Calcule a fração do total da turma que escolheu uma das cores.
C) Calcule a fração da turma que não escolheu nenhuma das cores.
QUESTÃO 4
Para fazer a cobertura de um bolo, Ana Maria usou
- 3/8 de uma barra de chocolate ao leite e
- 2/8 de uma barra de chocolate meio amargo
Sabendo que as duas barras são iguais em tamanho e peso, podemos afirmar que Ana Maria usou o equivalente a
(A) menos de uma barra de chocolate.
(B) uma barra de chocolate.
(C) duas barras de chocolate.
(D) sete barras de chocolate.
QUESTÃO 5
Você gosta de desafios? Aqui tem três para você.
Leia com atenção, pense e responda.
A) Escreva uma soma de frações cujo resultado seja 7/9.
B) Escreva uma subtração de frações cujo resultado seja 3/10.
C) Escreva uma soma ou subtração de frações, com denominadores diferentes, cujo resultado seja ⅝.
| Autoria | Cristiane Soares de Souza |
| Formação | Matemática – Licenciatura |
| Componente curricular | Matemática |
| Habilidade(s) | (EF06MA21) Construir figuras planas semelhantes em situações de ampliação e de redução, com o uso de malhas quadriculadas, plano cartesiano ou tecnologias digitais. |
| Objeto(s) de conhecimento | Conceito de fração; tipos de fração; adição e subtração de frações (com mesmo denominador e denominadores diferentes). |
| Descritor | D22 – Identificar fração como representação que pode estar associada a diferentes significados. |
| Referência(s) | SILVEIRA, Ênio. Matemática: compreensão e prática. 5ª edição, São Paulo, Moderna, 2018. BRASIL, EMBRAPA, Contando ciência na WEB. Água. Disponível em https://www.embrapa.br/contando-ciencia/agua/-/asset_publisher/EljjNRSeHvoC/content/vamos-economizar-agua-/1355746?inheritRedirect=false#:~:text=Para%20saber%20quais%20s%C3%A3o%20eles,%22A%20terra%20%C3%A9%20azul%22., acesso em 16/06/25. |

