Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 5º Período (7ª Série) da Educação de Jovens e Adultos – EJA

Reconhecendo os números racionais
Pense em um número, é quase certeza que, neste momento da sua vida curricular, este número é um NÚMERO RACIONAL. Mas quem são eles?
Os números racionais estão presentes em todos os momentos das nossas vidas, com exceção daqueles profissionais que se utilizam de cálculos mais avançados na elaboração de projetos.
Na imagem temos vários exemplos de números racionais. Mas como defini-los?
Definição de números racionais
Os números racionais são todos aqueles que podem ou que já estão escritos na forma de uma fração. Eles são encontrados expressos na forma de porcentagem, de número inteiro, de decimal exata e periódica.
Veja alguns exemplos:
- Paulo gasta 40% do seu salário com aluguel.
- Júlia comeu 3/8 de pizza.
- Pedro gastou R$35,99 na compra de 1kg de carne.
- O número da residência da Maria é o 176.
- Paulo dividiu 20 reais para 3 pessoas e obteve R$6,666… e aproximou para R$6,67.
Mas por quê 40%, R$35,90, e 176 são números racionais se eles não estão expressos na forma fracionária?
Para responder a esta questão, basta fazer as transformações e simplificações já estudadas.
- 40% é o mesmo que:
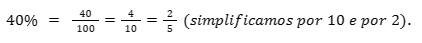
- 35,90 pode ser escrito como:
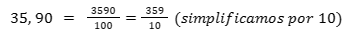
- e o número 176 é só acrescentar 1 no denominador, ou seja:
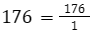
E quando os números racionais estão na forma de uma decimal periódica?
Veja o exemplo de como transformá-lo em uma fração.
Ao dividir 1 por 2, obtemos a decimal periódica 0,3333…., então 0,333… é o mesmo que:
- 0,333…=1/2
Mas ficou fácil, já sabíamos a fração!
Então, como devo fazer para determinar a fração que representa a decimal periódica 0,666…?
Neste caso vamos seguir os passos:
- chamar de x a decimal periódica: x = 0,666….
- multiplicar tudo por 10: 10x = 6,666….
- subtrair os resultados dos dois itens: 9x = 6.
- e finalmente, divida tudo por 9: x = 6/9.
Portanto a decimal periódica 0,666…, pode ser representada pela fração 6/9.
Veja o vídeo no saiba mais sobre fração geratriz.
Em resumo, todo número que pode ser escrito na forma de fração é um número racional.
Ficamos por aqui.
Atividades
QUESTÃO 01
Na sequência a seguir, a alternativa que contém apenas números racionais expressos como decimais exatos é:
(A) 32 ; 7,85 e 6,777…
(B) 8,93 ; 5,75 e 3,555…
(C) 2,5 ; 83 e 3,87
(D) 3,77 ; 5,67 e 8,4
QUESTÃO 02
Para transformar um número racional expresso na forma fracionária para a forma decimal, basta realizar a divisão do numerador pelo denominador. Sabendo disso, faça essa transformação para os números abaixo:

QUESTÃO 03
Sobre os números racionais, podemos afirmar que:
(A) Todo número racional pode ser expresso, somente, na forma de decimal exata.
(B) Os números racionais podem ser expressos na forma de decimal exata ou periódica.
(C) Os números racionais não podem ser expressos na forma de porcentagem.
(D) Uma fração não é um número racional.
QUESTÃO 04
Observe a tabela de gastos do Sr. João no mês de fevereiro de 2023.
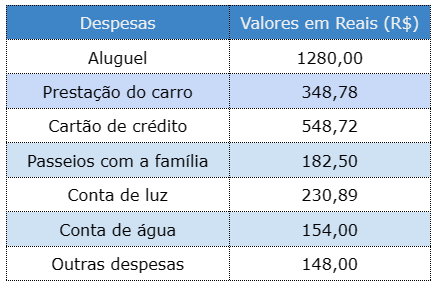
Agora responda:
(A) Quais dos itens relacionados têm valores expressos na forma de número inteiro?
(B) Quais dos itens relacionados têm valores expressos na forma de decimal exata?
(C) Qual foi o gasto total das despesas do Sr. João neste mês.
SAIBA MAIS
Quer saber um pouco mais sobre números racionais? Então assista aos vídeos do canal do Prof. Hélio
Fração de uma decimal periódica
Operações com números racionais na forma decimal – cálculo do IMC.
| Autoria | Prof. Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Objetivos de Aprendizagem e Desenvolvimento: | (EJAMA0504) Reconhecer que os números racionais positivos podem ser expressos nas formas: fracionária, percentual, decimal exata e decimal não exata (dízima periódica). |
| Referências | GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 7° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. |

