Matemática – Um pouco dos Trapézios

Esta proposta de atividade de Matemática é destinada aos estudantes do 4º Período da Educação de Jovens e Adultos – EJA.

Definição

Um trapézio é um quadrilátero que possui exatamente dois lados paralelos. Esses lados paralelos são chamados de bases do trapézio. As bases podem ter comprimentos diferentes, e os outros dois lados do trapézio são chamados de lados não paralelos ou lados oblíquos.

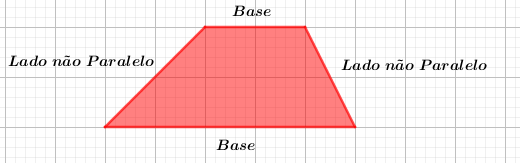
Imagem do Autor produzida no Geogebra

Elementos do Trapézio

Os principais elementos do trapézio são:

• Bases: os dois lados paralelos do trapézio.
• Lados oblíquos: os dois lados não paralelos do trapézio.
• Altura: a distância perpendicular entre as duas bases.
• Diagonais: os segmentos de reta que unem vértices opostos do trapézio.

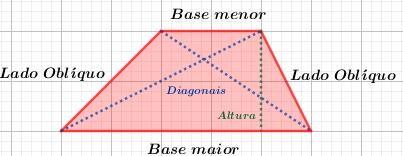
Imagem do Autor produzida no Geogebra

Classificação dos Trapézios

Os trapézios podem ser classificados de acordo com suas características específicas:

• Trapézio retângulo: são aqueles que possuem dois ângulos retos.
• Trapézio isósceles: são aqueles em que os lados oblíquos têm a mesma medida.
• Trapézio escaleno: são aqueles em que todos os lados têm medidas diferentes.

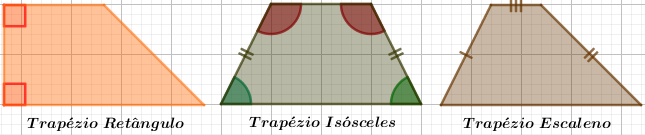
Imagem do Autor produzida no Geogebra

Trapézios no dia a dia

Os trapézios estão presentes em diversas situações do nosso dia a dia, por exemplo:

• Nos objetos de uso pessoal: caixas de presente, bolsas e outros objetos.
• Na construção civil: prédios, fachadas, janelas, luminárias, telhados e outros.
• Na natureza: em formações rochosas, cristais e folhas de algumas plantas.

Imagem do canva.com/trapézios

Conclusão

Os trapézios são figuras geométricas versáteis e presentes em diversas situações do nosso dia a dia. Ao compreender suas características e propriedades, podemos apreciar melhor a beleza e a funcionalidade dessas formas geométricas.

Atividade

QUESTÃO 01

Um trapézio é um quadrilátero que possui exatamente

(A) 1 par de lados paralelos.

(B) 2 pares de lados paralelos.

(C) 3 lados paralelos.

(D) Nenhum lado paralelo.

QUESTÃO 02

Um trapézio isósceles é caracterizado por ter

(A) todos os lados congruentes.

(B) apenas um par de lados opostos congruentes.

(C) os lados não paralelos congruentes.

(D) as bases congruentes.

QUESTÃO 03

Um terreno tem formato de trapézio isósceles. A base maior mede 30 metros, a base menor mede 20 metros e um dos lados não paralelos mede 13 metros. Deseja-se construir uma cerca ao redor do terreno. Qual será o comprimento total da cerca?

QUESTÃO 04

Imagine que você tenha um terreno com formato de trapézio retângulo para construir sua casa. As medidas desse terreno são:

• Frente do terreno (base maior): 60 metros
• Distância do fundo ao muro da frente (altura): 20 metros
• Lado inclinado do terreno (lado oblíquo): 25 metros
• Fundo do terreno (base menor): metade da frente

Para construir uma cerca ao redor do terreno, você precisará de arame farpado. Considerando que você dará 5 voltas de arame:

A) Qual é a medida do fundo do terreno?

B) Quantos metros de arame você precisará no total?

OBS. Faça um desenho para representar o problema.

SAIBA MAIS

Quer saber um pouco mais sobre os trapézios? Então só clicar no vídeo.

---

Autoria	Professor Hélio Roberto da Rocha, Mestre em matemática
Componente curricular	Matemática
Objetivos de aprendizagem e desenvolvimento	(EJAMA0426) Identificar as características dos quadriláteros, classificá-los em relação a lados e ângulos e reconhecer a inclusão e a intersecção de classes entre eles.
Referências	SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9° ano – Ensino Fundamental; Matemática; Goiânia,2024.