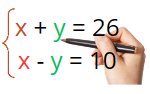Matemática – Os sistemas de equações e o método da adição

Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 5º período (7ª série) da Educação de Jovens e Adultos – EJA

Se não existirem multiplicação, divisão, potenciação ou radiciação envolvendo essas incógnitas, dizemos que os sistemas são lineares.

Exemplos:

Para que servem os sistemas de equações?

O principal objetivo dos sistemas de equações é o de facilitar a resolução de problemas mais complexos, por exemplo:

Você está comprando maçãs e bananas em uma feira. As maçãs custam R$2,00 cada e as bananas custam R$1,50 cada. Você comprou um total de 10 frutas e gastou R$15,00. Quantas maçãs e bananas você comprou?

Esse exemplo mostra que saber resolver um sistema de equações pode ser útil para determinar a quantidade de diferentes itens comprados, levando em consideração os custos e as quantidades totais.

Como resolver um sistema de equações do 1° grau?

Existem alguns métodos:

• Método da Adição. 
• Método da Substituição.
• Método da Comparação.

Neste texto, abordaremos o Método da Adição.

Em que consiste o Método da Adição?

O método da adição é uma técnica utilizada na resolução de sistemas de equações lineares que envolve a adição ou subtração das equações de forma a eliminar uma das incógnitas, permitindo assim encontrar o valor das demais incógnitas.

O procedimento básico é:

• escolher uma das incógnitas para eliminar através da soma ou subtração das equações (de preferência a que possui coeficiente 1);
• obter uma nova equação em que a incógnita escolhida seja eliminada;
• resolver essa equação, determinando o valor de uma das incógnitas;
• substituir o valor encontrado em uma das equações originais e determinar o valor da outra incógnita.

Vamos a um exemplo:

Compra de ingressos

Paula planeja comprar ingressos para um show. O preço de um ingresso para adultos é de R$40,00, enquanto o preço de um ingresso para crianças é de R$20,00. Paula precisa comprar um total de 10 ingressos e gastar exatamente R$300,00. Quantos ingressos de cada tipo você deve comprar para atender a essas condições?

Chamando de x o número de ingressos de adultos e y o de crianças, teremos o seguinte sistema:

Se adicionarmos ou subtrairmos as duas equações, não eliminaremos uma das incógnitas, para isso vamos multiplicar a (1) por – 20, obtendo assim um novo sistema equivalente:

Somando as duas equações:

20x = 100 ( dividindo por 20 obtemos o valor de x).

x = 5

Substituindo o valor de x = 5 na equação (1) determinamos o valor de y.

5 + y = 10

y = 5

Portanto, Paula deve comprar 5 ingressos para adultos e 5 para crianças.

Ficamos por aqui, até o próximo.

Atividades

QUESTÃO 01

O Sr. Hélio sacou R$110,00 em um caixa eletrônico. Essa quantia era composta apenas de cédulas de 10 e 20 reais, em um total de 8 cédulas. Considerando x o número de cédulas de 10 reais e y o número de cédulas de 20 reais, podemos afirmar que, o sistema de equações que permite determinar o número de cédulas de cada valor que o Sr. Hélio sacou é o

QUESTÃO 02

Utilize sistemas de equações do 1º grau para resolver o seguinte problema.

Um pai tem o dobro da idade de seu filho. A soma das idades deles é 36 anos. Quantos anos cada um tem?

QUESTÃO 03

Uma loja vende camisetas e bonés. O preço de uma camiseta é de R$30,00 e o preço de um boné é de R$20,00. Comprando 5 peças e pagando um total de R$120,00, o cliente levará

(A) 2 camisetas e 3 bonés.

(B) 3 camisetas e 2 bonés.

(C) 4 camisetas e 1 boné.

(D) 1 camiseta e 4 bonés.

QUESTÃO 04

Utilize o método da adição para determinar a solução do sistema de equações de 1º grau.

SAIBA MAIS

Aprenda um pouco mais sobre sistemas de equações de 1° grau assistindo o vídeo do canal do prof. Hélio no YouTube.

Autoria	Prof. Hélio Roberto da Rocha, Mestre em Matemática
Componente Curricular	Matemática
Objetivos de aprendizagem e desenvolvimento	(EJAMA0512) Interpretar e resolver situações-problema que necessitam ser representados por sistemas de equações de 1º grau com duas incógnitas, diferenciando e utilizando os métodos de resolução.
Referências	SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024.