Olá, educando (a)! Esta videoaula de Matemática para a 8ª série da Eaja foi veiculada na TV no dia 10/06/2021 (Quinta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.

Nessa atividade você fará um estudo sobre semelhança de triângulos, nela você irá perceber como este conteúdo é utilizado no campo da engenharia de construção civil.
Assista a videoaula a seguir, com a temática: Semelhança de Triângulos
Olá, como você está? Espero que esteja bem.
Hoje você irá trabalhar um tema da unidade de Geometria, a Semelhança de Triângulos. Podemos ver esse assunto em profissões que se utilizam do cálculo como, por exemplo, as engenharias e arquiteturas.
Um dos monumentos mais conhecidos e visitados no mundo é a torre Eiffel, que fica em Paris, na França. Essa torre foi inaugurada em 1889, até então a torre mais alta do mundo. No município brasileiro de Umuarama (PR) foi construída uma réplica da torre em uma escala de 1:10. Uma construção semelhante à original. Assim como a torre Eiffel, temos também o Cristo Redentor.
Antes de começar com alguns conceitos, vou propor a você um problema que poderemos encontrar no nosso dia a dia.
O problema é determinar a altura de um prédio. Se usássemos uma fita métrica ou uma trena, seria muito complicado. O assunto de hoje irá facilitar a resolução.
Problema proposto: Um prédio projeta no solo uma sombra de 30 m de extensão no mesmo instante em que uma pessoa de 1,80 m projeta uma sombra de 2,0 m. Determinar a altura do prédio.
Veja a figura.
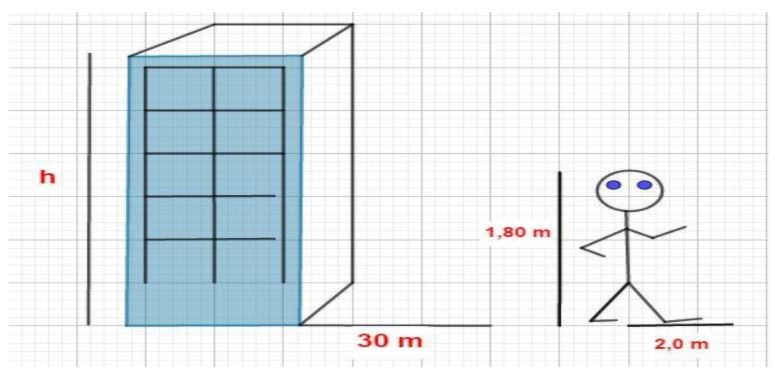
Para resolver este problema, necessitamos de algum conhecimento sobre semelhança de triângulos. Então vamos para os conceitos.
Semelhança (do dicionário informal): algo parecido, semelhante. Por exemplo as duas sandálias de um par, são semelhantes.
Polígonos semelhantes (definição): dois polígonos são semelhantes se os ângulos internos correspondentes forem congruentes e os lados correspondentes proporcionais entre si.
Relação de proporcionalidade (definição): uma relação de proporcionalidade quer dizer que se dividirmos a medida de um lado de uma figura pela medida de um lado, correspondente, da outra figura e o resultado for, por exemplo, 5, então todas as divisões entre as medidas dos lados da primeira figura com os lados correspondentes da segunda figura deverão ser iguais a 5. Esse valor denominamos de constante de proporcionalidade.
Resumindo
Para que dois polígonos sejam semelhantes é necessário que exista uma proporcionalidade entre seus lados correspondentes e os ângulos, também correspondentes, sejam congruentes (mesma medida).
Observe na figura abaixo dois polígonos semelhantes, neles a constante de proporcionalidade é igual a 2. Se você dividir as medidas dos lados correspondentes você irá encontrar 2. As medidas dos ângulos, correspondentes, são congruentes.
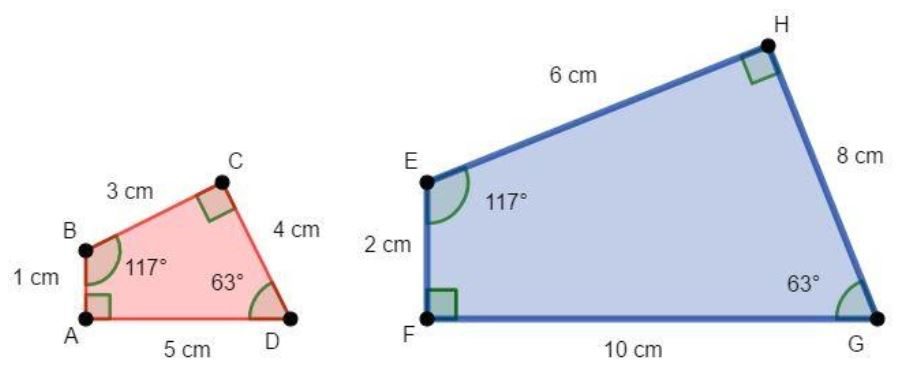

Os ângulos são congruentes:
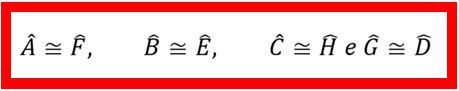
Semelhança de triângulos (definição):dois triângulos são semelhantes, quando os seus três ângulos (ordenadamente) forem congruentes e seus lados, correspondentes, forem proporcionais. Os lados correspondentes são chamados de lados homólogos, ou seja, lados opostos aos ângulos correspondentes.
Observe na figura abaixo dois triângulos semelhantes, a constante de proporcionalidade é igual a 3, se você dividir as medidas dos lados correspondentes você irá encontrar 3. As medidas dos ângulos, correspondentes, são congruentes.
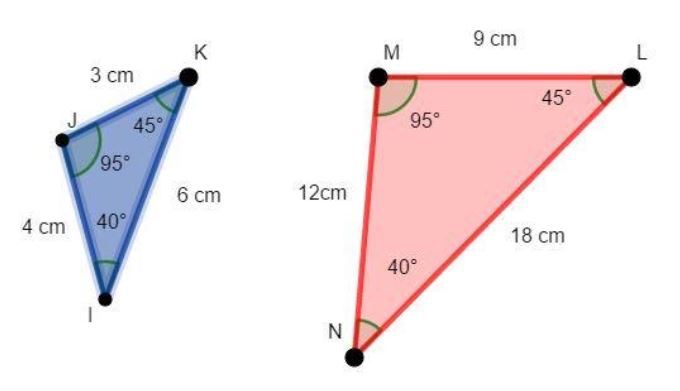

Os ângulos são congruentes
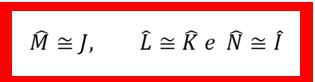
Casos de Semelhança de Triângulos
1º Caso AA (Ângulo, Ângulo): dois triângulos são semelhantes, se dois ângulos de um forem congruentes a dois ângulos do outro.
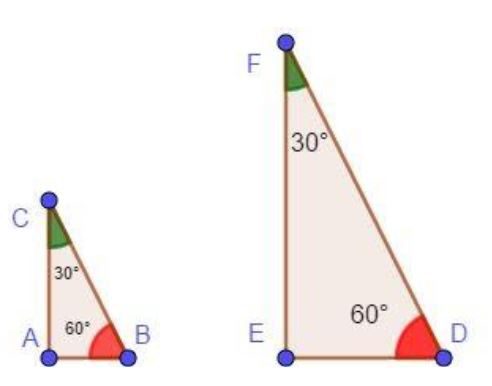
2º Caso LLL (Lado, Lado, Lado): dois triângulos são semelhantes se os três lados de um são proporcionais aos três lados do outro.
Observe que a constante de proporcionalidade é igual a 2.
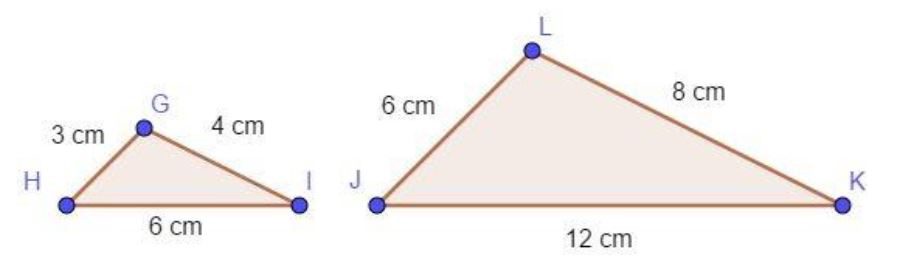
3º Caso LAL (Lado, Ângulo, Lado): dois triângulos são semelhantes se possuem um ângulo congruente compreendido entre lados proporcionais.
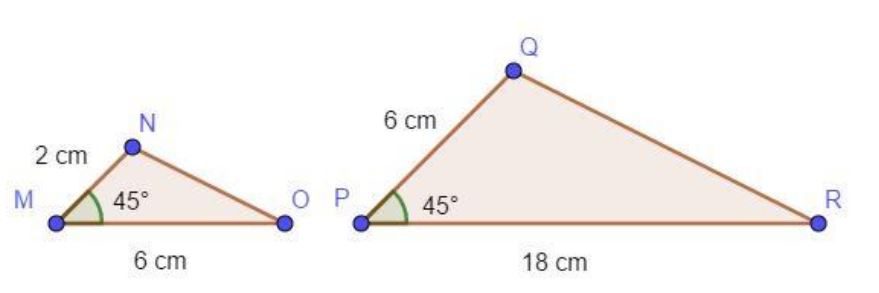
Se a razão de semelhança entre dois triângulos for igual a 1, então podemos afirmar que os triângulos são congruentes.
Lembra quando dois triângulos são congruentes? Vou te ajudar:
Congruência de Triângulos: dois triângulos são congruentes quando as medidas dos seus lados e dos seus ângulos, correspondentes, são congruentes (mesma medida)
Relação entre os perímetros de triângulos semelhantes
Se dois triângulos forem semelhantes de modo que a razão de semelhança seja k, então a razão entre os seus perímetros será também igual a k.
Chamando P de perímetro, teremos:

Só para lembrar: o perímetro de um triângulo é a soma das medidas dos seus três lados.
Como ilustração dessa propriedade, considere os triângulos do 2º caso de congruência (LLL), nele podemos determinar os seus perímetros.
Perímetro 1 = 3+4+6= 13 e Perímetro 2 = 6+8+12=26. A constante de proporcionalidade é igual a 2.
Se dividirmos P1 por P2, obtemos 2 que é o mesmo valor da constante de proporcionalidade.
Relação entre as áreas de triângulos semelhantes
Se dois triângulos forem semelhantes de modo que a razão de semelhança seja k, então a razão entre as suas áreas é dada pelo quadrado da razão de semelhança entre eles.
Chamando A de área, teremos:
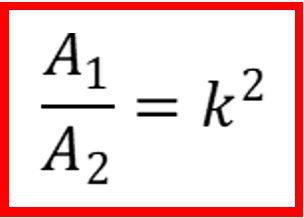
Agora para fechar, vou resolver o problema do início desta atividade.
Para determinar a altura desse prédio, um engenheiro poderá usar a semelhança de triângulos. Imagine que o prédio, sua sombra projetada e o raio solar formam um triângulo, da mesma forma, temos também um triângulo formado pela pessoa, sua sombra e o raio solar. Considerando que os raios solares são paralelos e que o ângulo entre o prédio e o solo e a pessoa e o solo é igual a 90º, os triângulos, indicados na figura abaixo, são semelhantes pelo caso AA (dois ângulos iguais). Logo podemos afirmar que:
A altura do prédio está para a altura da pessoa, assim como a sombra do prédio está para a sombra da pessoa. Escrevendo uma equação, podemos determinar a altura do prédio.
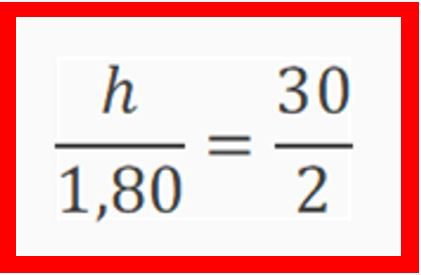
Dividindo 30 por 2 e multiplicando o resultado por 1,80, obtemos 27. Logo a altura do prédio é igual a 27 metros. Como, em média, o pé direito de um apartamento é em torno de 2,10m, esse prédio tem, aproximadamente, 10 andares.
Assista aos vídeos do canal do Prof. Hélio para aprender como determinar a altura de um prédio.
Para finalizar, vou deixar este problema para você.
A sombra de uma árvore, em um terreno plano, em uma determinada hora do dia, mede 3,40 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de 1,40 m de altura mede 0,60 m. Determinar a altura da árvore, em metros.
Veja a figura
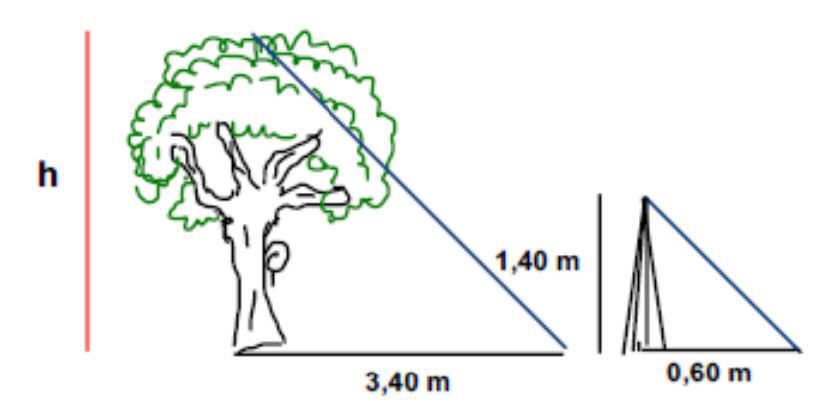
Assista ao vídeo do canal do Prof. Hélio para aprender como determinar a altura de uma árvore.
Bom, ficamos por aqui. Espero ter ajudado você nesse conteúdo bastante importante da matemática. Abraços e até a próxima.
| Objetivos de Aprendizagem e Desenvolvimento | (EF09MA12-B) Reconhecer triângulos semelhantes em situações de ampliação, congruência e redução, e as relações que existem entre seus perímetros e suas áreas. |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).
