Esta proposta de atividade de Matemática é destinada aos estudantes do 6º Período (8ª série) da Educação de Jovens e Adultos – EJA.

Introdução
O círculo é uma figura geométrica simples, mas muito presente em nosso dia a dia, sendo encontrada em objetos como moedas, botões e CDs. Neste texto iremos apresentar sua definição, seus elementos e como calcular a medida da sua área, além de 2 problemas resolvidos.
Imagem: canva.com/https://l1nk.dev/rTmQD
Definição e Elementos de um Círculo
Um círculo é a região plana limitada por uma circunferência. Ele possui um raio, que é a distância do centro do círculo até qualquer ponto da sua circunferência.
Seus principais elementos são:
- Centro: ponto dentro do círculo de onde todas as distâncias até a circunferência são iguais.
- Circunferência: linha curva que delimita o círculo.
- Raio: segmento de reta que une o centro do círculo a um ponto qualquer da circunferência.
- Diâmetro: segmento de reta que passa pelo centro do círculo e tem suas extremidades na circunferência. É o dobro do raio.
Veja na imagem esses elementos
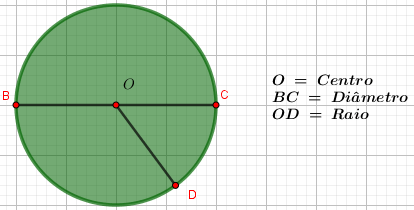
Imagem do Autor produzida no Geogebra
Área do Círculo
A área do círculo é a medida da sua região interna. Para calcular a área de um círculo, utilizamos a fórmula:
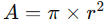
Onde:

Problemas de Aplicação
Problema 1
Alice tem um espelho circular, como o da figura abaixo, onde a parte espelhada possui 40cm de diâmetro. Ela decidiu decorar a moldura do espelho com adesivos decorativos, mas quer ter certeza de que não cobrirá a área útil do espelho. Qual é a área da superfície do espelho que Alice pode usar para se ver refletida?

Resolução:
Aplicando a fórmula que calcula a medida da área e considerando o valor do pi aproximadamente igual a 3,14, teremos:
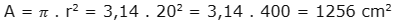
Imagem: canva.com/https://l1nk.dev/rTmQD
Lembrando que a medida do raio é igual à metade da medida do diâmetro.
Resposta:
A medida da área da superfície do espelho que Alice pode usar é de 1256 cm2 .
Problema 2
João possui um jardim com canteiros circulares de raio 3 metros. Ele deseja comprar adubo para cobrir a área de todos os canteiros. Sabendo que cada metro quadrado requer 1 kg de adubo, quantos quilogramas de adubo João deve comprar?

Resolução:
Aplicando a fórmula que calcula a medida da área e considerando o valor do pi aproximadamente igual a 3,14, teremos:
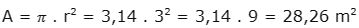
Imagem: canva.com/https://l1nk.dev/rTmQD
Resposta:
Como cada metro quadrado requer 1 kg de adubo, João deve comprar 28,26 kg de adubo.
Para finalizar, quero deixar aqui registrado a importância de se conhecer a fórmula da área de regiões circulares, pois permite resolver diversas situações que nos deparamos no nosso dia-a-dia que envolva objetos circulares.
Ficamos por aqui, até o próximo.
OBS. Em todas as questões, utilizar o valor do pi igual a 3.
QUESTÃO 01
Maria tem um jardim circular com raio de 5 metros. Ela deseja colocar um círculo de pedras decorativas ao redor das rosas, com um raio de 7 metros. Quantos metros quadrados de pedras ela precisa para completar o círculo externo?
QUESTÃO 02
Uma medalha olímpica tem a forma de um círculo com diâmetro de 5 centímetros. Qual é a área da medalha?
QUESTÃO 03
Uma horta circular tem um raio de 6 metros. Se você deseja colocar esterco na horta você irá precisar de
(A) 78 metros quadrados.
(B) 88 metros quadrados.
(C) 108 metros quadrados.
(D) 110 metros quadrados.
QUESTÃO 04
A área de um espelho circular de 60 centímetros de diâmetro é igual a
(A) 2500 cm².
(B) 2600 cm².
(C) 2650 cm².
(D) 2700 cm².
SAIBA MAIS
Aprenda um pouco mais sobre comprimento e área de círculo.
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0617) Resolver situações-problema envolvendo o cálculo das medidas do comprimento da circunferência e área do círculo. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. |
