Matemática – Resolvendo Problemas com Sistemas de Equações

Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 5º período da Educação de Jovens e Adultos – EJA

Definição de Sistemas de Equações do 1º Grau

Um sistema de equações do 1º grau é um conjunto de duas ou mais equações lineares com duas ou mais incógnitas. Essas equações representam situações em que duas ou mais variáveis estão relacionadas entre si. A solução de um sistema é o conjunto de valores que satisfazem todas as equações do sistema simultaneamente.

Elementos de um Sistema de Equações

• Equações: as expressões algébricas separadas por uma igualdade.
• Incógnitas: as variáveis que queremos encontrar o valor.
• Coeficientes: os números que multiplicam as incógnitas.
• Termos independentes: os números que não acompanham as incógnitas.

Exemplo:

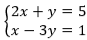
Neste sistema, as equações são 2x+y=5 e x-3y=1, as incógnitas são x e y, os coeficientes são 2, 1, 1 e -3, e os termos independentes são 5 e 1.

Como resolver um Sistema de Equações?

Existem diversos métodos para resolver sistemas de equações do 1º grau. Dois dos mais comuns são:

Método da Substituição:

• Isolamos uma das incógnitas em uma das equações.
• Substituímos a expressão encontrada na outra equação.
• Resolvemos a equação resultante para encontrar o valor de uma das incógnitas.
• Substituímos o valor encontrado na equação inicial para encontrar o valor da outra incógnita.

Método da Adição:

• Multiplicamos as equações por números convenientes para que os coeficientes de uma das incógnitas se anulem quando as equações forem somadas ou subtraídas.
• Somamos ou subtraímos as equações para eliminar uma das incógnitas.
• Resolvemos a equação resultante para encontrar o valor de uma das incógnitas.
• Substituímos o valor encontrado em uma das equações iniciais para encontrar o valor da outra incógnita.

Problemas Resolvidos

Problema 1 

A soma de dois números é 20. A diferença entre eles é 4. Quais são esses números?

Solução: 

Considerando x e y os dois números desconhecidos, podemos escrever o sistema:

Resolvendo pelo método da adição:

Somando as equações, eliminamos a incógnita y e determinamos a incógnita x:

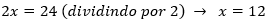
Substituindo x por 12 na equação (1), determinamos o valor de y

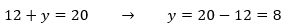
Resposta:

Os números são 12 e 8.

Problema 2

Um pai tem o triplo da idade de seu filho. Daqui a 5 anos, a soma de suas idades será 50 anos. Quais são as idades atuais do pai e do filho?

Solução: 

Considerando p a idade do pai e f a idade do filho, podemos escrever o sistema:

Resolvendo o sistema pelo método da substituição:

Substituindo p por 3f na equação (2):

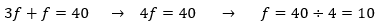
Substituindo f por 10 na equação (1):

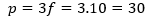
Resposta:

O pai tem 30 anos e o filho tem 10 anos.

Conclusão

Os sistemas de equações do 1º grau são ferramentas poderosas para resolver problemas de diversas áreas e com a prática, você se tornará cada vez mais habilidoso na resolução desses sistemas.

Ficamos por aqui, até o próximo.

Atividade

QUESTÃO 01

Em uma granja, há galinhas e coelhos. Ao todo, são 20 cabeças e 56 pés. A quantidade de galinhas nessa granja é

(A) 8.

(B) 10. 

(C) 12.

(D) 14.

QUESTÃO 02

Um pai tem o triplo da idade de seu filho. Daqui a 5 anos, a soma de suas idades será 50 anos. A idade atual do filho é

(A) 8 anos.

(B) 9 anos. 

(C) 10 anos.

(D) 11 anos.

QUESTÃO 03

Para a festa de aniversário de Pedro, sua mãe comprou pizzas e refrigerantes. Sabendo que cada pizza custou R$30,00 e cada refrigerante R$3,00, e que foram gastos R$180,00 no total. Além disso, a quantidade de refrigerantes comprados foi o dobro da quantidade de pizzas.

A) Monte um sistema de equações que represente essa situação, considerando x como a quantidade de pizzas e y como a quantidade de refrigerantes. 

B) Resolva o sistema e determine quantas pizzas e refrigerantes foram comprados.

QUESTÃO 04

Uma loja de celulares vende dois modelos de smartphones: o modelo A e o modelo B. Em um determinado dia, foram vendidos 50 celulares no total, gerando uma receita de R$45.000,00. Sabendo que o modelo A custa R$ 1.000,00 e o modelo B custa R$900,00,

A) Escreva um sistema de equações que represente a situação, considerando x como a quantidade de celulares do modelo A vendidos e y como a quantidade de celulares do modelo B vendidos. 

B) Resolva o sistema e determine quantos celulares de cada modelo foram vendidos.

SAIBA MAIS

Assista ao vídeo para aprender um pouco mais sobre Sistemas de Equações do 1º grau.

Autoria	Professor Hélio Roberto da Rocha, Mestre em Matemática.
Componente Curricular	Matemática
Objetivos de aprendizagem e desenvolvimento	(EJAMA0512) Interpretar e resolver situações-problema que necessitam ser representados por sistemas de equações de 1o grau com duas incógnitas, diferenciando e utilizando os métodos na resolução.
Referências	SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9º ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9° ano – Ensino Fundamental; Matemática; Goiânia, 2024.