Olá! Esta aula de Matemática é destinada aos educandos da 5ª Série da Eaja.
Na aula de hoje você estudará as operações de adição e subtração no conjunto dos números naturais, aprenderá sobre as suas propriedades e resolverá situações-problema envolvendo essas duas operações.
Assista à videoaula do professor Hélio Rocha com a temática adição e subtração.
Adição
A adição é uma das primeiras operações estudadas, e está associada à ideia de acrescentar, de aumentar, de crescer, de juntar dois ou mais elementos de um mesmo conjunto. Ela é bastante usada em nosso cotidiano, por exemplo, ao realizar as compras em um supermercado.
Veja um exemplo
Paulo foi ao supermercado e gastou R$ 18,00 em verduras, R$ 154,00 em carnes e R$ 36,00 em frutas. Quantos reais Paulo gastou?
A ideia aqui é juntar, somar esses valores. Veja como fazer essa adição utilizando a decomposição dos números e em seguida utilizando um algoritmo.
Usando a decomposição

Usando o algoritmo usual

Resposta do problema: Paulo gastou R$ 208,00.
Atividade 1
Um jovem vendendo camisetas no primeiro dia do trabalho, recebeu R$ 95,00, no segundo dia R$ 135,00 a mais que o primeiro dia, e no terceiro dia recebeu R$ 6,00 a mais que no fim do segundo dia. Quanto recebeu ao todo?
Propriedades da Adição

Elemento Neutro
Em uma adição de duas parcelas, quando uma delas é zero, a soma é igual à outra parcela. Logo podemos dizer que o ZERO é o ELEMENTO NEUTRO da adição.
Exemplos
35 + 0 = 35 0 + 9 = 9 12 + 0 = 12
Subtração
A subtração é uma operação matemática que indica quanto é o resultado de um valor (minuendo) se dele for removido, tirado, subtraído, outro valor (subtraendo). Esse resultado, denominamos de diferença ou resto.
Veja um exemplo
Em uma fábrica, foi produzida em um dia 975 peças. Houve um problema em uma das máquinas e 186 peças saíram com defeito. Quantas peças foram produzidas sem defeito?
Exemplo clássico de subtração. Iremos resolver por decomposição e por algoritmo usual.
Usando a decomposição

Explicando
Fig. 1. Não é possível retirar 6 de 5 e nem 80 de 70. Fazemos a decomposição
Fig. 2. Não é possível retirar 80 de 60, fazemos novamente a decomposição.
Fig. 3. Agora só subtrair.
Usando o algoritmo usual
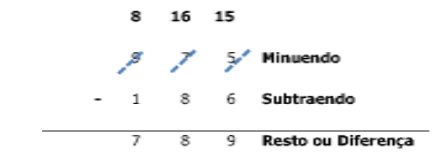
Resposta do problema: Foram produzidas 789 peças sem defeito.
Nos exemplos acima, pode-se identificar a ideia de adição e subtração como operações inversas.
Atividade 2
O consumo de energia elétrica na casa de Luciana nos meses de abril e maio foram de 282kWh e 189kWh, respectivamente. Determine:
- Quantos quilowatts-hora (kWh) foram reduzidos no consumo desses dois meses.
- Na casa do seu irmão, Pedro, foram consumidos 197kWh no mês de abril e em maio foram consumidos 48kWh. Quantos quilowatts-hora foram consumidos em maio na casa de Pedro?
Relação envolvendo adição e subtração
Veja as situações-problema.
- Pensei em um número, adicionei 90 a ele, e obtive 120. Em que número pensei?
Podemos representar esse problema por meio de uma adição, onde uma das parcelas é desconhecida e iremos chama-la de x para representar o número pensando.
x + 90 = 120
Para determinar o valor de x basta utilizar a subtração:
x = 120 – 90 = 30
Portanto o número pensado é igual a 30.
- Pensei em um número, subtraí 70 dele e obtive 50. Em que número pensei.
Podemos representar esse problema por meio de uma subtração, onde uma o minuendo será o número que pensei e que iremos chama-lo de x e o subtraendo o 70.
x – 70 = 50
Para determinar o valor de x basta utilizar a adição:
x = 50 + 70 = 120
Resposta: o número pensado é igual a 120.
Atividade 3
Alguns desafios para você! Resolva as questões a seguir para checar o que você aprendeu. Use os exemplos acima e o vídeo do professor Hélio Rocha para esclarecer dúvidas, caso precise.
- Tenho R$ 1225,00 para comprar um celular, mas ainda me falta R$ 820,00. Qual é o preço do celular?
- A distância de Recife até Exu, cidade do sertão pernambucano, onde nasceu Luiz Gonzaga, é de 630 km e de Petrolina a Exu é de 258 km. Qual a distância de Petrolina a Recife, passando por Exu?
- (A Conquista da Matemática, José Ruy Giovanni Júnior, p39, 6ano) O governo organiza, periodicamente, campanhas de vacinação contra a paralisia infantil. Numa dessas campanhas, em determinado município, foram vacinadas 11 296 crianças do centro urbano e 1 649 crianças da área rural. Quantas crianças foram vacinadas nesse município?
4.(Saresp-SP _ Adaptada) A tabela mostra a distribuição dos alunos dos 3 turnos de uma escola, de acordo com o sexo.

É correto afirmar que:
a) todos os turnos têm o mesmo número de alunos.
b) a escola tem um total de 360 alunos.
c) o número de mulheres é maior que o de homens.
d) o noturno tem 230 alunos.
5.Um automóvel custa, à vista, 54 680 reais e, a prazo, 76 270 reais. A diferença entre esses valores equivale ao juro que se paga pelo financiamento. Se uma pessoa comprar esse automóvel a prazo, que quantia pagará de juro?
6.(Unicamp-SP) Minha calculadora tem lugar para 8 algarismos. Eu digitei nela o maior número possível, do qual subtraí o número de habitantes do estado de São Paulo, obtendo, como resultado, 63 033 472. Qual era a população do estado de São Paulo nesse ano?
Chegamos ao final de mais uma aula. Abraços e até a próxima!
| Referência | Sousa, Joamir Roberto de – Matemática realidade & tecnologia: 6º ano |
| Componente Curricular | Objetivo de aprendizagem e desenvolvimento |
| Matemática | (EAJAMA0505) Interpretar, resolver e elaborar situações-problema que envolvam cálculos com números naturais, com compreensão dos processos neles envolvidos. |

