Esta proposta de atividade de MATEMÁTICA é destinada aos estudante do 6º Período da Educação de Jovens e Adultos–EJA
Introdução
Neste texto exploraremos as condições de semelhança de triângulos destacando os casos de semelhança, a definição de razão de semelhança e três problemas práticos para ilustrar esses conceitos.
Imagem produzida no canva.com/https://l1nk.dev/ojB23
Triângulos Semelhantes
Triângulos são semelhantes quando possuem os mesmos ângulos e os lados correspondentes proporcionais. Isso significa que, embora os tamanhos dos triângulos possam ser diferentes, suas formas são idênticas.
Casos de Semelhança de Triângulos
- AA (Ângulo – Ângulo)
Dois triângulos são semelhantes se dois ângulos de um triângulo forem congruentes a dois ângulos do outro triângulo.
- LAL (Lado – Ângulo – Lado)
Dois triângulos são semelhantes se dois lados de um triângulo forem proporcionais a dois lados do outro triângulo e o ângulo entre esses lados for congruente.
- LLL (Lado – Lado – Lado)
Dois triângulos são semelhantes se os três lados de um triângulo forem proporcionais aos três lados do outro triângulo.
Razão de Semelhança
Razão de semelhança é a razão entre os lados correspondentes de dois triângulos semelhantes.
Se a razão de semelhança é k, então todos os lados de um triângulo são k vezes os lados correspondentes do outro triângulo.
Problemas e Resolução
Problema 1:
Uma torre projeta uma sombra de 40 m. No mesmo momento, uma vara de 1 m projeta uma sombra de 0,8 m. Qual é a altura da torre?
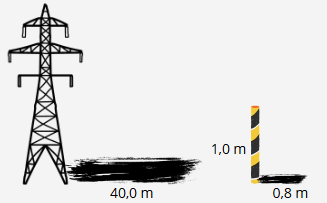
Imagem Produzida no canva.com
Resolução: Os triângulos formados pela vara e sua sombra e pela torre e sua sombra são semelhantes (AA).
Razão de semelhança: k = 40/0,8 = 50.
A altura da torre: h = 50 . 1 = 50 metros
Resposta: A altura da torre é de 50 metros.
Problema 2: Um prédio projeta uma sombra de 18 m. Ao mesmo tempo, uma árvore de 2 m projeta uma sombra de 3 m. Qual é a altura do prédio?
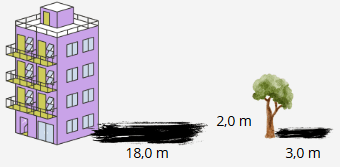
Imagem Produzida no canva.com
Resolução: Os triângulos formados pela árvore e sua sombra e pelo prédio e sua sombra são semelhantes (AA).
Razão de semelhança: k = 18/3 = 6.
Altura do prédio: h = 6 . 2 = 12 metros.
Resposta: A altura do prédio é de 12 metros.
Problema 3: João está subindo uma rampa inclinada. A rampa tem uma altura total de 6 metros. Quando João havia percorrido 3 metros da rampa, ele estava a 2 metros de altura. Usando o conceito de semelhança de triângulos, determine a distância que falta para João percorrer até alcançar o topo da rampa.
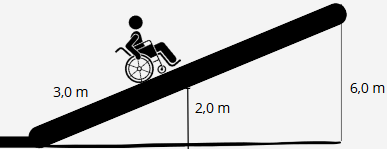
Imagem Produzida no canva.com
Resolução: Os triângulos formados pela rampa e pela parte percorrida por João são semelhantes (AA).
Razão de semelhança: k= 6/2 = 3.
Comprimento da Rampa: x = 3 . 3 = 9 metros.
Distância que falta para percorrer = 9 – 3 = 6 metros.
Resposta: A distância que falta para João percorrer até alcançar o topo da rampa é de 6 metros.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
João deseja saber a altura de uma árvore em seu quintal. Ele mede uma sombra de 2 metros de um poste de 1,5 metros de altura. No mesmo momento, ele mede a sombra da árvore que é de 6 metros.

Imagem produzida no canva.com.br
(A) Qual é a altura da árvore?
(B) Se a sombra do poste aumentar para 3 metros, qual será a nova altura da árvore, mantendo a proporção?
QUESTÃO 02
Carlos observa dois triângulos semelhantes (figura), um menor com lados de 3 centímetros, 4 centímetros e 5 centímetros, e outro maior com um dos lados correspondentes de 10 centímetros.
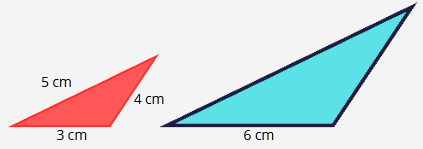
Imagem produzida no canva.com.br
A) Qual é o comprimento do lado correspondente maior do segundo triângulo?
B) Qual é o comprimento do lado correspondente médio do segundo triângulo?
QUESTÃO 03
Paulo observa que uma vara de 2 metros projeta uma sombra de 1 metro. No mesmo momento, um poste projeta uma sombra de 3 metros. A altura do poste, para manter a proporção, é
(A) 3 metros.
(B) 4 metros.
(C) 6 metros.
(D) 5 metros.
QUESTÃO 04
Marcos quer saber a altura de uma torre. Ele mede uma vara de 1,5 metros que projeta uma sombra de 2 metros. No mesmo instante, a torre projeta uma sombra de 8 metros. A altura da torre, mantendo a semelhança, é
(A) 4 metros.
(B) 6 metros.
(C) 10 metros.
(D) 12 metros.
SAIBA MAIS
Aprenda um pouco mais sobre o assunto assistindo o vídeo do canal do Prof. Hélio no YouTube
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0618) Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes (destacando os casos de semelhança), em situações de ampliação, congruência e redução, e as relações que existem entre seus perímetros e suas áreas. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. |
