Olá! Esta aula de Matemática é destinada a educandos da 5ª Série da Eaja.
Na aula de hoje você aprenderá o básico sobre frações no conjunto dos números naturais, tais como: equivalência, comparação, operações de adição, subtração e o cálculo da fração de um número natural.
ASSISTA A VIDEOAULA ABAIXO COM A TEMÁTICA – COMPREENDENDO AS FRAÇÕES
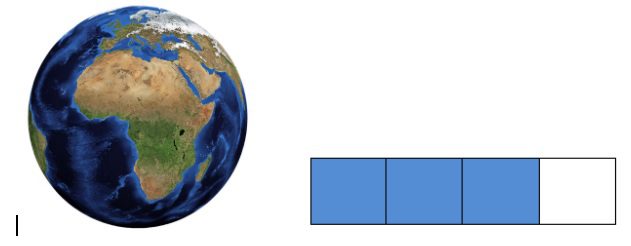
O astronauta Yuri Gagarin, ao observar a Terra do espaço, disse que ela era azul. Se representarmos a superfície da Terra por meio de uma figura dividida em quatro partes, veremos que três partes correspondem à parte coberta de água.
A parte azul da figura corresponde à parte da superfície da Terra coberta de água, ou seja, 3 partes de 4. Podemos representar a parte da superfície da Terra coberta por água por meio de uma fração, veja:
O numerador indica quantas partes foram consideradas e o denominador indica quantas partes iguais a unidade foi dividida. A leitura dessa fração é feita como “três quartos”.
Já deu para ter noção do que é uma fração? Ainda não? Então vamos a definição. Fração é a representação das partes de um objeto dividido em partes iguais, ou uma divisão em que o numerador representa o dividendo e o denominador o divisor. Veja mais um exemplo para entender melhor, observe a imagem abaixo:

Cada uma das figuras acima, foi dividida em partes iguais e a fração é representa pela parte destacada de azul. A primeira figura foi dividida em 6 partes iguais e foram coloridas 3 partes, por isso o numerador é 3 (quantas partes foram consideradas) e o denominador é 6 (quantas partes iguais a unidade foi dividida). A segunda figura foi dividida em 12 partes iguais e foram coloridas 8 partes, por isso o numerador é 8 (quantas partes foram consideradas) e o denominador é 12 (quantas partes iguais a unidade foi dividida). Já na figura 3 foi dividida em 9 partes iguais e foram coloridas 2 partes, por isso o numerador é 2 (quantas partes foram consideradas) e o denominador é 9 (quantas partes iguais a unidade foi dividida). Entendeu? Lembre-se, as leituras das frações são feitas assim: três sextos, oito doze avos e dois nonos.
Agora, se o numerador for maior do que o denominador, como seria a representação? Segue o exemplo, representado por meio de fração e de um número na forma mista, da parte destacada das figuras.
Imagem 1
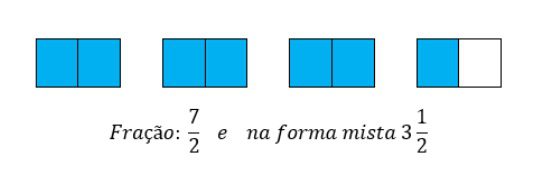
Na imagem 1 a unidade foi dividida em 2 partes, porém 7 pares foram consideradas, por isso foi preciso ter 3 unidades divididas em 2 partes. A forma mista é composta por uma parte inteira (3) e uma parte fracionária (1/2).
Imagem 2

Na imagem 2 a unidade foi dividida em 5 partes, porém 5 partes foram consideradas, por isso foi preciso ter 2 unidades divididas em 5 partes. A forma mista é composta por uma parte inteira (1) e uma parte fracionária (2/5).
Agora vamos falar sobre as frações escritas na forma decimal. Você já sabe que um número decimal é aquele número composto por uma parte inteira e uma decimal, separadas por uma vírgula, por exemplo: 3,82, onde a parte inteira é 3 e a parte decimal 82. Mas onde o estudo de frações entra nisso? Simples, você viu que as frações podem ser dadas pelo quociente entre dois números, o numerador e o denominador. Então vamos a alguns exemplos.
Veja alguns exemplos.

Na letra (b) temos o número 2,33333…. que denominamos de decimal periódica, pelo motivo da divisão nunca ter um resto igual a zero e no quociente sempre aparecer o 3 (período).
Como fazer para saber qual fração representa a maior quantidade? Para responder a essa pergunta é necessário fazer a comparação de frações. E para comparar duas frações, ou seja, ver qual representa a maior ou a menor quantidade, é preciso obter uma fração equivalente (são aquelas escritas de forma diferente, mas que representam a mesma quantidade) ou simplificar uma fração, ou seja, escrevê-la na forma mais simplificada possível (com o menor numerador e denominador).
As imagens a seguir representam folhas de papel sulfite divididas em partes iguais. Na figura 1 a folha foi dividida em 2 partes, na figura 2 em 4 partes e na figura 3 em 8 partes, todas iguais. Em todas elas foram pintadas a metade do total de partes. Observe as frações obtidas.
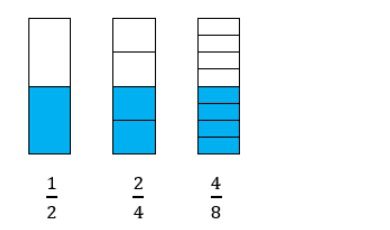
Note que essas frações representam a mesma parte das folhas. Nesse caso dizemos que elas são frações equivalentes. Podemos escrever que:

Para obtermos frações equivalentes, basta dividir ou multiplicar o numerador e o denominador por um mesmo número. Para simplificar frações, basta dividir o numerador e o denominador por um mesmo número. Ao simplificar uma fração, obtemos uma fração irredutível. Veja os exemplo a seguir:
- Obter 4 frações equivalentes da fração 2/3
- Simplificar as frações 8/12 e 18/48.
No exemplo 1, basta você multiplicar a fração por qualquer número natural que você queira. No exemplo 2, a simplificação de 18/48 ocorre igual mostra a imagem abaixo:
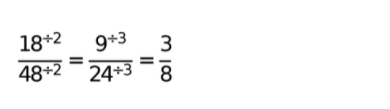
Observe que no início é simplificado tudo por 2 e depois, o resultado por 3, chegando a uma fração irredutível. Isso significa que 18/48 (dezoito quarenta e oito avos) representa a mesma quantidade que 3/8 (três oitavos).
E agora, como calcularíamos uma fração de um número natural? Por exemplo 2/3 de 12 reais. Simples! Basta dividir o 12 por 3 e multiplicar o resultado por 2, logo o resultado será: 12:3=4 e 4×2=8, ou seja, 8 reais. Vamos a outro exemplo bem:
15 colegas de trabalho resolveram fazer uma aposta e premiar aqueles que mais acertassem os resultados dos jogos de um campeonato de futebol. Sabendo que cada pessoa contribuiu com 20 reais e que os prêmios seriam distribuídos da seguinte forma:
- 1º primeiro colocado: 1/2 do valor arrecadado;
- 2º primeiro colocado: 1/3 do valor arrecadado;
- 3º primeiro colocado: recebe a quantia restante.
Quanto, respectivamente, cada participante premiado recebeu? Consegue fazer esse cálculo? Para fazer essa conta, primeiro calculamos o valor total do prêmio, dado por: 15×20=300 reais. Depois calculamos a premiação, sendo que para o 1º colocado, como ele recebeu 1/2 do valor arrecadado, divide-se 300 por 2 e multiplica por 1, resultando 150 reais; para o 2º colocado, como ele recebeu 1/3 do valor arrecado, divide-se 300 por 3 e multiplica por 1, resultando 100 reais; e o terceiro colocado, como recebe a quantia restante, faturou 50 reais.
ATIVIDADE 1
Em um desses finais de semana, você, sua esposa e seus 2 filhos, compraram uma pizza tamanho gigante cortada em 20 pedaços iguais. Se você comer 2/5 e sua esposa 1/5 da pizza, quantos pedaços sobraram para os seus 2 filhos? Responda em seu caderno.
ATIVIDADE 2
Responda, em seu caderno, o valor das seguintes adições e subtrações de fração.
ATIVIDADE 3
João Carlos é operário e seu salário é de apenas 1520 reais por mês. Gasta 1/4 com aluguel
e 2/5 com alimentação da família. Esse mês ele teve uma despesa extra e 3/8 do seu salário foram gastos com remédios. Sobrou dinheiro?
Assista aos vídeo no canal do Prof. Hélio, disponibilizados nos links abaixo, para ver resoluções de atividades parecidas com estas aqui propostas. Link 1: https://youtu.be/5IcspgveP9U Link 2: https://youtu.be/COv1V9W3DSQ
Bom, vamos ficar por aqui, espero você na próxima aula. Abraços do Professor Hélio!
| Componente Curricular | Objetivos de Aprendizagem e Desenvolvimento |
| Matemática | (EAJAMA0513) Compreender, comparar e ordenar frações associadas às ideias de partes de inteiros e resultado de divisão, identificando frações equivalentes. (EAJAMA0514) Reconhecer que os números racionais podem ser expressos nas formas fracionária e decimal, estabelecer relações entre essas representações. (EAJAMA0515) Resolver situações-problema que envolvam o cálculo da fração de uma quantidade e cujo resultado seja um número natural. (EAJAMA0516) Resolver problemas que envolvam adição ou subtração com números racionais na representação fracionária |