Matemática – A Potenciação e suas propriedades

Esta proposta de atividade de Matemática é destinada aos estudantes do 6º Período (8ª série) da Educação de Jovens e Adultos – EJA.

POTENCIAÇÃO

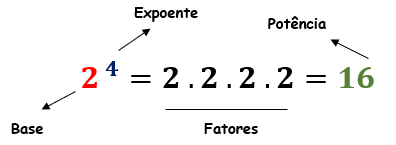
Nomenclatura

O que vem a ser isso?

São as denominações que damos a cada termo da potenciação. 

Na potenciação 2⁴ = 2 . 2 . 2 . 2 = 16 (aqui utilizamos o ponto para representar a multiplicação), temos:

Propriedades das potências

Em matemática, as propriedades são afirmações verdadeiras que podem ser comprovadas, provadas. Basicamente, servem para reduzir os cálculos e simplificar as expressões.

P1: Multiplicação de potências de mesma base

Como resolver essa expressão 2³ . 2² – 1 ?

Podemos determinar o resultado de 2³ e 2² depois multiplicá-los e subtrair 1, ou podemos aplicar P1.

Em uma multiplicação de potências de mesma base, conservamos a base e somamos os expoentes.

A solução da expressão fica:

Com a P1: 2³ . 2² -1 = 2³⁺² -1 = 2⁵– 1 = 32 – 1 = 31.

Sem a P1: 2³ . 2² -1 = 8.4 -1 = 32 – 1 = 31.

As duas formas são tranquilas!

P2: Divisão de potências de mesma base.

Como resolver essa expressão 3¹⁸ : 3¹⁶ – 1 ?

Neste caso, se formos calcular 3¹⁸ e 3¹⁶  seria um processo bem trabalhoso e fácil de se errar. Melhor aplicar a P2.

Em uma divisão de potências de mesma base, conservamos a base e subtraímos os expoentes.

A solução da expressão com a P2 fica: 

3¹⁸ : 3¹⁶ – 1 = 3^18-16 – 1= 3² – 1 = 3.3 – 1 = 9 – 1 = 8.

P3: Potência de potência.

Como resolver essa expressão (5²)³ – 1 ?

Aqui pode-se calcular a potência 5² e o resultado elevar ao cubo e depois retirar 1. Ficando assim:

(5²)³ – 1 = 25³ – 1 = 25.25.25 -1 = 15625-1=15624 

Ou podemos aplicar a P3.

Em uma potência de potência, podemos repetir a base e multiplicar os expoentes.

E a expressão fica:

(5²)³ – 1 = 5⁶ – 1 = 5.5.5.5.5.5 – 1 = 15625 – 1 = 15624.

As duas maneiras são parecidas no nível de dificuldade.

Alguns resultados (R) que podemos destacar na potenciação.

R1: Todo número diferente de 0 (zero) elevado a zero é igual a 1.

a) 3⁰ = 1 b) 67⁰ = 1 c) (-3)⁰ = 1

R2: Todo número elevado a 1 (um) é igual ao próprio número.

a) 3¹ = 3 b) 600¹ = 600 c) (-5)¹ = -5

R3: Se a base for um expoente negativo, devemos invertemos a base e trocar o sinal do expoente para positivo.

Para compreender melhor este resultado, assista o vídeo do canal do prof. Hélio.

Atividades

QUESTÃO 01

Sabendo que A = 5³ – 12 e B = 2² +12, pede-se:

A) Leia a expressão A e escreva-a como se lê.

B) Leia a expressão B e escreva-a como se lê.

C) O valor de A.

D) O valor de B.

E) A diferença entre A e B.

B) A soma entre A e B.

QUESTÃO 02

Para determinar a área de um terreno quadrado, ou seja, a quantidade de metros quadrados que ele possui, basta elevar a medida do seu comprimento ao quadrado. Sabendo disso, determinar a área de um terreno quadrado cuja lateral mede

A) 7 metros.

B) 12 metros.

D) 15 metros.

QUESTÃO 03

Utilizando as propriedades da potenciação, podemos afirmar que o resultado da expressão 2²⁸ : 2²⁵ – 1 é igual a

(A) 5.

(B) 7.

(C) 8.

(D) 9.

QUESTÃO 04

A chácara do Sr. Paulo possui 8 pés de laranjas. Em um certo dia ele contou e verificou que em cada árvore existia 8 galhos e em cada galho 8 laranjas. Podemos afirmar que na chácara do Sr. Paulo, nesse dia, existiam

(A) 64 laranjas.

(B) 24 laranjas.

(C) 512 laranjas.

(D) 612 laranjas.

Autoria	Professor Hélio Roberto da Rocha, Mestre em Matemática.
Componente Curricular:	Matemática
Objetivos de Aprendizagem e Desenvolvimento:	(EJAMA0604) Efetuar cálculos com números reais, inclusive com radicais, usando propriedades operatórias, racionalização de denominadores, na resolução de situações problema diversos.
Referências	SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 8º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 8° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018.