Olá! Esta aula de Matemática é destinada aos educandos da 7ª Série da Eaja.
Nesta aula você irá compreender a relação entre a potenciação e a radiciação, além de compreender o cálculo de uma potência com expoente fracionário.

Assista à videoaula a seguir com a temática potência com expoente inteiro positivo e expoente fracionário.
Como você assistiu na vídeoaula do professor Hélio Rocha, a Potenciação é uma operação de multiplicação de fatores iguais. Sendo a um número racional e n um número natural, com a diferente de zero, temos:

Alguns valores notáveis
- Em uma potência com expoente 1 e a base um número racional qualquer, o resultado é esse próprio número.
- Em uma potência com expoente 0 e a base um número racional qualquer diferente de zero, o resultado é 1.
ATENÇÃO!!!
Fique atento para não confundir potenciação e multiplicação. A potenciação é uma multiplicação de fatores iguais e a multiplicação é a adição de parcelas iguais.
Atividade 1
Escreva por extenso as potências indicadas a seguir e depois resolva-as. A letra (a) será o exemplo que você deverá seguir.
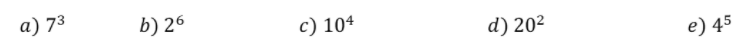
A leitura de 73 é : sete elevado a terceira potência ou sete ao cubo e o resultado dessa potência é dado por: 7.7.7 = 343.
Agora é com você! Escreva por extenso as demais potências.
Um outro exemplo envolvendo a potenciação.
- Como calcular o volume de um cubo de aresta 6 cm?
Um cubo é uma figura que faz parte da geometria espacial e é caracterizado como um poliedro com 6 faces congruentes. O cálculo do volume de um cubo é dado pelo valor da aresta ao cubo. Para calcular o volume de um cubo de 6cm de aresta, basta realizar a potenciação 63 = 6.6.6 = 216 cm3.
Radiciação é a operação inversa da potenciação. Enquanto a potenciação procura determinar o produto dos fatores iguais, a radiciação procura determinar esses fatores.
Veja um exemplo
Ao determinarmos o número que multiplicado por ele mesmo resulta 400, obtemos a raiz quadrada de 400, que pode ser indicada da seguinte maneira:
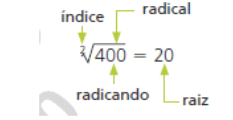
Lê-se: a raiz quadrada de 400 é igual a 20.
Quando se trata de raiz quadrada, não é necessário indicar o índice.
Porque a radiciação é uma operação inversa da potenciação?
Veja os exemplos

Uma aplicação de radiciação, está no cálculo de área e medida de lados de objetos retangulares.
Veja um exemplo.
Você já aprendeu que para determinar a área de um quadrado basta elevar a medida do lado ao quadrado.

Como a potenciação é a operação inversa da radiciação, podemos escrever que a medida do lado do quadrado é igual a raiz quadrada da medida de sua área. Portanto a medida do lado será:

Atividade 2
Calcule:

Potência com expoente fracionário
Como você pode calcular uma potência cuja base é um número positivo e o expoente é um número racional na forma de fração?
Observe o exemplo
Para calcular a potência 53/2
Considere x = 53/2, vamos elevar o primeiro e o segundo membro ao quadrado.

Uma regra para simplificar
Para resolver potências com expoente fracionário, basta convertê-las em raízes, onde o radicando será a base da potência, o índice do radical será o denominador da fração e o expoente do radicando, o numerador da fração.
Aplicando a regra
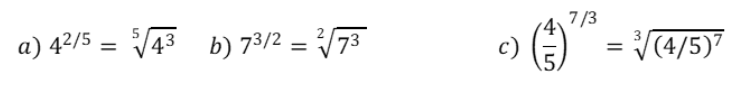
Você observou que a base da potência ficou sendo o radicando, o denominador o índice e o numerador o expoente do radicando?
Atividade 3
Calcule as potências. Simplifique o resultado final.

Bom, finalizamos por aqui, espero sua participação na próxima atividade. Abraços e até a próxima.
| Referência | Sousa, Joamir Roberto de – Matemática realidade & tecnologia: 8º ano. |
| Componente Curricular | Objetivo de aprendizagem e desenvolvimento |
| Matemática | (EAJAMA0704) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário. |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).
