Esta proposta de atividade de Matemática é destinada aos estudantes do 6º Período da Educação de Jovens e Adultos – EJA.
Introdução
Neste texto, vamos explorar o Teorema de Pitágoras, um dos conceitos fundamentais da geometria, que nos permite entender a relação entre os lados de um triângulo retângulo. Começaremos com uma breve introdução ao matemático grego Pitágoras e sua contribuição para a matemática, seguida pelo enunciado formal do teorema. Em seguida, apresentaremos dois problemas práticos resolvidos que ilustram como o Teorema de Pitágoras pode ser aplicado em situações do dia a dia.
Imagem do autor produzida no Geogebra
Uma Ferramenta Essencial na Geometria
O Teorema de Pitágoras, uma das mais famosas e importantes relações matemáticas, é fundamental para a compreensão da geometria e possui inúmeras aplicações práticas em diversas áreas do conhecimento. Ele estabelece uma relação fundamental entre os lados de um triângulo retângulo e é atribuído ao matemático grego Pitágoras, que viveu por volta de 570 a.C.
O Enunciado do Teorema de Pitágoras
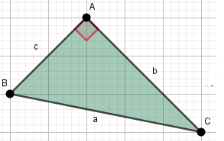
Em um triângulo retângulo, o quadrado da medida da hipotenusa (lado oposto ao ângulo reto) é igual à soma dos quadrados das medidas dos catetos (os outros dois lados).
Em linguagem matemática:
Se a, b e c são as medidas dos lados de um triângulo retângulo, sendo a a hipotenusa, então:
Imagem do autor produzida no Geogebra
Problemas de Aplicação
Problema 1: Medindo a Diagonal de um Terreno
Imagine que você tem um terreno retangular e precisa descobrir a medida da sua diagonal. Se os lados do terreno medem 30 metros e 40 metros, qual será a medida da diagonal?
Imagem do autor produzida no Geogebra
Resolução:
Aplicando o Teorema de Pitágoras:
Portanto, a diagonal do terreno mede 50 metros.
Problema 2: Altura de uma Escada Encostada na Parede
Uma escada de 13 metros está encostada em uma parede. Se a base da escada está a 5 metros de distância da parede, qual é a altura que a escada atinge na parede?
Resolução:
Neste caso, a escada é a hipotenusa, a distância da base à parede é um dos catetos, e a altura que a escada atinge é o outro cateto.
Aplicando o Teorema de Pitágoras:
Assim, a escada atinge uma altura de 12 metros na parede.
Para finalizar
Conhecer o Teorema de Pitágoras é essencial, pois ele nos permite solucionar problemas práticos envolvendo distâncias e medidas em diversas áreas, como construção civil e engenharia. Para você, estudante, dominar esse conceito é um passo importante para desenvolver habilidades matemáticas que serão úteis tanto nos estudos quanto em futuras carreiras profissionais.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
Construindo uma cerca
Um pedreiro precisa construir uma cerca para delimitar um terreno triangular. Dois lados desse terreno medem 5 metros e 12 metros, formando um ângulo reto entre eles.
A) Qual será o comprimento do terceiro lado da cerca?
B) Se cada metro de cerca custa R$ 20,00, qual será o valor total da cerca?
QUESTÃO 02
Um bombeiro precisa resgatar uma pessoa que está em um prédio em chamas. Para isso, ele precisa usar uma escada que, quando apoiada no chão, forma um ângulo de 90° com o muro. A base da escada está a 8 metros de distância do muro e a parte superior da escada alcança 15 metros de altura.
A) Qual é o comprimento da escada?
B) Se o bombeiro subir pela escada a uma velocidade de 1 metro por segundo, quanto tempo ele levará para alcançar o topo?
QUESTÃO 03
Um pedreiro precisa construir uma rampa para acesso a um palco. A rampa deve ter 3 metros de comprimento e 1 metro de altura. A distância horizontal da base da rampa até o palco é de, aproximadamente
(A) 2 metros.
(B) 2,8 metros.
(C) 3 metros.
(D) 4 metros.
QUESTÃO 04
Um ciclista percorre 12 km para o leste e depois 9 km para o norte. A distância em linha reta entre o ponto de partida e o ponto de chegada é de
(A) 3 km.
(B) 15 km.
(C) 21 km.
(D) 10 km.
SAIBA MAIS
Assista o vídeo para aprender um pouco mais sobre o Teorema de Pitágoras.
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0620) Interpretar, resolver e elaborar situações-problema envolvendo relações métricas no triângulo retângulo e as relações de proporcionalidade nas retas paralelas cortadas por secantes. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6° ao 9º ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. |

