Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 5º período da Educação de Jovens e Adultos – EJA
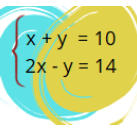
Introdução
O objetivo ao resolver um sistema de equações com duas ou mais incógnitas, é determinar os valores das incógnitas que satisfazem todas as equações simultaneamente. Existem alguns métodos para se determinar esses valores e, neste texto, estudaremos o método da substituição.
Imagem: Produzida no canva.com/https://l1nk.dev/GuUxR
Definição de Sistemas de Equações (SE) de 1º Grau
Um sistema de equações do 1º grau é um conjunto de duas ou mais equações lineares com duas ou mais variáveis.
OBS. Equações Lineares são equações de primeiro grau (expoente igual a 1) com uma, duas ou mais variáveis.
Exemplos de SE:
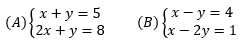
Os sistemas de equações podem ser escritos a partir de uma informação.
Por exemplo:
Paula está comprando maçãs e peras. Cada maçã custa R$2,00 e cada pera custa R$3,00. Paula comprou um total de 15 frutas e gastou R$38,00. Podemos criar um sistema de equações para representar essa situação e determinar o número de maçãs e peras que Paula comprou, veja:
Considerando m para representar o número de maçãs e p o número de peras que Paula comprou, teremos:
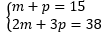
O Método da Substituição (MS)
Passos para a resolução de um sistema utilizando o MS:
Passo 1: Escolher uma equação (a que for mais simples) e isolar uma variável.
Passo 2: Substituir a expressão obtida na outra equação. Obtendo uma equação com 1 só variável.
Passo 3: Resolver a equação obtida no item 2.
Passo 4: Substituir o valor encontrado no passo 3 na equação obtida no passo 1.
Passo 5: Pronto. Se quiser pode verificar se a solução está correta substituindo os valores encontrados nas equações originais para garantir que eles satisfazem todas as equações do sistema.
A solução do sistema é um par ordenado, as letras em ordem alfabética, escrito na forma: S={(__ , __)}.
Exemplo 1
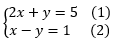
Passo 1:Isolando y na equação (1): y = 5 – 2x
Passo 2 e 3: Substituindo y na equação 2 e resolvendo:
x – (5 – 2x) = 1
x – 5 + 2x = 1
3x = 1 + 5
3x = 6
x = 2
Passo 4: Substituindo esse valor na equação obtida no passo 1:
y = 5 – 2x
y = 5 – 2.2
y = 1
A solução do sistema: S={(2,1)}
Exemplo 2
Resolvendo o sistema para determinar a quantidade de maçãs e de peras do exemplo acima.
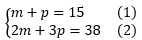
Passo 1: Isolando p na equação (1): p = 15 – m
Passo 2 e 3: Substituindo p na equação 2 e resolvendo:
2m + 3(15 – m) = 38
2m + 45 – 3m = 38
– m = 38 – 45
– m = – 7
m = 7
Passo 4: Substituindo esse valor na equação obtida no passo 1:
p = 15 – m
p = 15 – 7
y = 8
A solução do sistema: S={(7,8)} isso significa que Paula comprou 7 maçãs e 8 peras.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
Usando as letras x e y para representar as incógnitas (números desconhecidos), estabeleça um sistema de duas equações do 1° grau associado a cada uma das seguintes situações:
A) Julia tem 8 cédulas, umas de 10 reais e outras de 5 reais, perfazendo um total de 50 reais.
B) Duas camisetas custam juntas 120 reais e o preço de uma delas é o dobro da outra.
QUESTÃO 02
Considere a seguinte informação:
“ Em um sítio há bois e patos, totalizando 95 animais e 240 pernas”
Considerando que x representa o total de bois e que y representa o total de patos, podemos afirmar que o sistema de equações do 1º grau que melhor representa a informação é
QUESTÃO 03
Estabeleça um sistema de equações do 1° grau para a situação a seguir e, depois, utilizando o método da substituição, resolva o problema.
“A idade de Paula é o dobro da idade de Pedro, os dois juntos somam 102 anos. Determine a idade de Paulo e de Paula”.
QUESTÃO 04
A solução do sistema de equações do 1° grau
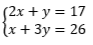
é igual a
(A) x = 5 e y = – 7.
(B) x = -5 e y = 7.
(C) x = – 5 e y = – 7.
(D) x = 5 e y = 7.
SAIBA MAIS
Assista ao vídeo para aprender um pouco mais sobre Sistemas de Equações do 1º grau.
| Autoria | Professor Hélio Roberto da Rocha, Mestre em Matemática. |
| Componente Curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0512) Interpretar e resolver situações-problema que necessitam ser representados por sistemas de equações de 1º grau com duas incógnitas, diferenciando e utilizando os métodos de resolução. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9º ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9° ano – Ensino Fundamental; Matemática; Goiânia, 2024. |
