Os números racionais

Os números racionais são todos os números que representam uma quantidade inteira, não inteira, negativa ou positiva. Eles podem vir escritos na forma de uma fração ou na forma decimal.
Imagem: canva.com.br/números
Veja alguns exemplos:
- 1 pacote de arroz, de 5kg, custa R$23,90.
- A temperatura na cidade de Toronto, no Canadá, neste momento, é de -4ºC.
- Em uma receita de um bolo de chocolate, acrescente 3 ovos, 1/2 de uma xícara uma chá, de óleo e 3/4 desta mesma xícara de leite.
- O saldo da conta bancária do Sr. José está no valor de -R$87,90 (saldo devedor).
Os números 1, 5 e 3 representam uma quantidade inteira e positiva, os números -4 e -87,90 (escrito na forma decimal) representam uma quantidade inteira negativa e uma não inteira também negativa, já os números 3/4 e 1/2 estão escritos na forma de fração. Todos eles pertencem ao conjunto dos números racionais.
Transformações
Em algumas situações costumamos fazer as transformações de um número racional na forma fracionária para a forma decimal e vice-versa.
Como fazer isso?
Forma Fracionária para a Decimal
Por exemplo:
Se você precisar saber quantos mililitros de leite existem em 3/4 de um litro, uma das maneiras de resolver essa situação é transformar a fração em decimal.
Neste caso dividimos 3 por 4 e depois multiplicamos o resultado por 1000, pois 1 litro de leite tem 1000 mL.
Veja o cálculo:
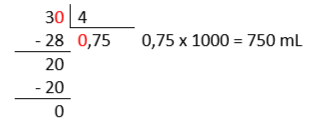
Neste tipo de transformação sempre iremos dividir o numerador pelo denominador, algumas vezes essa divisão poderá ser uma decimal exata ou uma decimal periódica. No exemplo temos uma decimal exata.
Um exemplo de decimal periódica:
Transformar a fração 2/3 em decimal.
Dividimos 2 por 3:
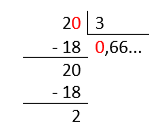
Percebemos que o 6 irá se repetir infinitamente, logo 2/3 = 0,66… é uma decimal periódica de período 6 (período é o algarismos que se repete).
Forma decimal para fracionária
Um dos objetivos de fazer essa transformação é o de comparar duas grandezas.
Por exemplo:
Paulo gasta 0,2 (dois décimos) do seu salário em passeios com a família. Se quiséssemos saber em quantas partes do seu salário, Paulo gasta com passeios, precisaríamos fazer a transformação da forma decimal para a fracionária.
Veja o cálculo:
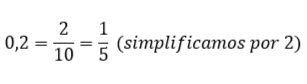
Portanto, Paulo gasta 1 parte do total de 5, em passeios com sua família.
Neste tipo de transformação sempre o denominador (divisor) será 10, 100, 1000, …, isso vai depender de quantas casas decimais (algarismos após a vírgula) tiver o número. No final simplificamos a fração, se possível.
No exemplo dividimos por 10 pois 0,2 possui 1 casas decimal e depois simplificamos a fração. Se caso fosse 0,02 seria dividido por 100 ou se fosse 0,002, por 1000.
Antes de começar a atividade, assista o vídeo para apreender como transformar uma decimal periódica em fração.
Atividade
QUESTÃO 01
Leia a receita de um bolo de chocolate com cenoura.
4 ovos
2 e 1/2 xícaras de chá de açúcar
4 colheres de sopa de manteiga sem sal
3/4 xícara de chá de óleo
200 ml de leite
3 e 1/2 xícaras de chá de farinha de trigo
1 xícara de chá de chocolate em pó
1 colher de sopa rasa de fermento em pó
4 cenouras, média, cortadas em cubos.
Agora, classifique cada número dessa receita em número natural, inteiro ou racional.
QUESTÃO 02
João trabalha como mecânico em uma oficina de sua cidade, seu salário é razoável. Infelizmente ele não tem casa própria e gasta, por mês, 2/5 do seu salário com aluguel, 1/3 com alimentação, 1/8 em diversão com a família e o restante ele guarda para outras ocasiões.
Em relação a essa situação, determine o número decimal que representa as frações do salário do João com:
A) alimentação.
B) aluguel.
C) diversão.
QUESTÃO 03
Os números decimais que representam as frações 3/5 , 6/8 e 5/9, são, respectivamente:
(A) 0,666… – 0,57 e 0,5.
(B) 0,57 – 0,666… e 0,5 .
(C) 0,6 – 0,75 e 0,5555….
(D) 0,555… – 0,75 e 0,6.
QUESTÃO 04
Um número racional escrito na forma decimal pode ser escrito na forma de fração irredutível. Por exemplo: 0,32 = 32/100 = 16/50 = 8/25 (simplificamos 3 vezes por 2). Sabendo dessa informação, os números 0,2; 0,35 e 0,484 escritos na forma de fração irredutível, nessa ordem, são:
(A) 1/5, 7/50 e 121/250.
(B) 2/5, 3/5 e 48/84.
(C) 2/5, 3/5 e 48/100.
(D) 2/10, 35/100 e 484/1000.
| Autoria | Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Objetivos de Aprendizagem e Desenvolvimento: | (EJAMA0602) Reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica (dízima periódica) e que pode ser escrita em forma de fração irredutível, localizando-os na reta numérica decompor e ordenar números naturais |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 8º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 8° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. |
