Olá, educando (a)! Esta videoaula de Matemática para a 8ª série da Eaja – foi veiculada na TV no dia 18/03/2021 (quinta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade você irá se familiarizar com os números racionais e irracionais, terá a oportunidade de reconhecer a importância desses números, suas formas de escritas e suas aplicações em situações problemas.
Quel tal? Vamos aprender um pouco mais sobre esse assunto pra lá de interessante?
Então pegue seu material e preste bastante atenção às explicações do professor Hélio Roberto da Rocha.
Olá, tudo bem com você?
O conhecimento sempre é importante para ajudar a entender e resolver os problemas do dia a dia. Hoje você vai aprender um pouco sobre os números, vamos especificar os diferentes conjuntos numéricos e o uso do número no nosso cotidiano.
Você já parou para pensar na quantidade de números que fazem parte do nosso dia a dia desde o momento que acordamos até o momento que vamos dormir. À medida que vamos evoluindo no conhecimento matemático, vamos necessitando de uma quantidade enorme de números para representar um valor exigido em determinados momentos.
Antes de partir para a atividade, gostaria que você acessasse o site TIC na Matemática, no link abaixo, para se familiarizar sobre a teoria dos conjuntos numéricos e os números no nosso cotidiano.
Link: A classificação dos números relacionada ao cotidiano – TIC na Matemática (ticsnamatematica.com)
Os Números no Nosso Cotidiano
De acordo com a leitura que você fez no site, podemos classificar os números em: naturais, inteiros, racionais, irracionais e reais. Temos outro conjunto chamado de números complexos, que futuramente você irá estudar.
Nesta atividade você irá focar nos números racionais e irracionais.
Você vai começar pelo seguinte problema.
Suponha que você esteja reformando a sua casa e terá que comprar uma quantidade de fio que deve passar pela diagonal do teto, de forma retangular, da sua sala. Supondo que o comprimento das paredes sejam de 4m de comprimento e 3m de largura, que por sinal é uma bela sala.
Observe a planta baixa na figura:
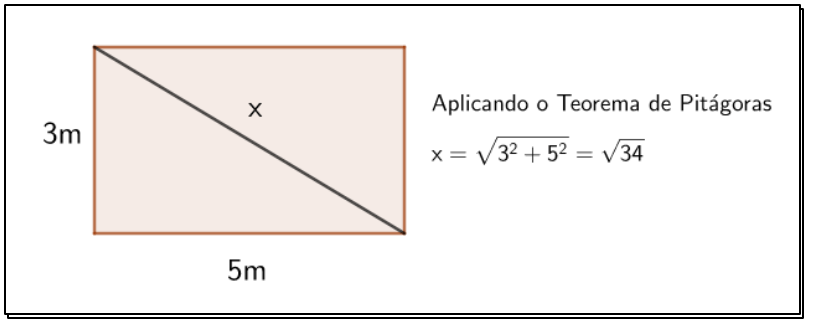
Este cálculo foi feito utilizando o famoso Teorema de Pitágoras.
Mais sobre Pitágoras no link: Quem foi Pitágoras? – Toda Matéria (todamateria.com.br)
Bom, neste ponto os matemáticos se depararam com a raiz quadrada de 34, esse número, na época de Pitágoras era um número que manchava a perfeição dos números e, portanto, não poderia existir. A partir daí se elaborou a teoria dos números irracionais.
Voltando ao problema, e extraindo a raiz quadrada de 34 obtemos o seguinte resultado 5,8309518948453… e o comprimento do fio será de aproximadamente 6 m.
Então, como podemos definir os números irracionais? Uma boa pergunta, para te responder precisamos definir os números racionais.
Pense em um número. Provavelmente, quase que certeza, esse número é um número racional. Os números racionais estão presente em quase tudo.
Por exemplo, nos preços de produtos de supermercado (os números decimais), no total de seguidores do seu Instagram (os números naturais), na medição da temperatura da vacina contra a Covid 19 da Pfizer (os números negativos, os chamados inteiros), na receita de bolo (os números fracionários).
Então, matematicamente falando, podemos definir os números racionais como:
Definição (Números Racionais): os números racionais (Q) são aqueles que podem ser escritos na forma de fração e que podem ser representados por uma decimal exata ou uma decimal periódica.
Exemplos:
- O número de alunos da turma da 8ª série do Eaja da Escola X é 32 (natural).
- Acrescente 3/4 (fração), de xícara de chá, de óleo.
- A temperatura de transporte e armazenamento da vacina contra Covid-19 da empresa Pfizer é de – 70° C (inteiro).
- Quando dividimos 20 reais para 3 pessoas encontramos o seguinte valor 6,6666666… (decimal periódica).
- O preço da vacina Astrazeneca/Oxford gira em torno de 2,5 euros que equivale a 14,90 reais (decimal exata).
Percebeu nos exemplos as formas em que aparecem os números racionais no nosso cotidiano.
Professor, então todos os números que conheço são racionais? Quase todos.
Os números que não aparecem neste conjunto, são os números irracionais. Veja a definição.
Definição (Números Irracionais)
os números irracionais (I) são números que não admitem serem escritos na forma de fração, pois em suas formas decimais, consistem em números infinitos não periódicos.
Podemos chegar a uma conclusão bem simples, que todos os números que extraímos raiz quadrada, cúbica, quarta, etc., que não der uma resposta exata, são exemplos de números irracionais.
Exemplos:
- Raiz quadrada de 2 é igual a 1,4142135623730950488016887242097…
- Raiz quadrada de 3 é igual a 1,7320508075688772935274463415059…
- Raiz cúbica de 9 é igual a 2,0800838230511904…
Percebe que todos eles a decimal não tem fim e não é periódica.
Existe um número irracional muito famoso, o número pi (π). Este número surgir na necessidade de determinar o comprimento da circunferência de latas, ou objetos, na forma de um cilindro.
O valor do número pi é um valor constante, ele é determinado pela divisão entre o comprimento da circunferência de um determinado objeto circular ou cilíndrico e seu diâmetro. Esse valor é dado por: 3,1415926535897932384626433832795… que é aproximamos por 3,14. Você observa que ele possui uma decimal infinita e não periódica.
Assista ao vídeo que preparei para você sobre o número pi.
Em resumo, podemos afirmar que todos esses números exemplificados são números reais. Assim chegamos a uma organização dos conjuntos numéricos.
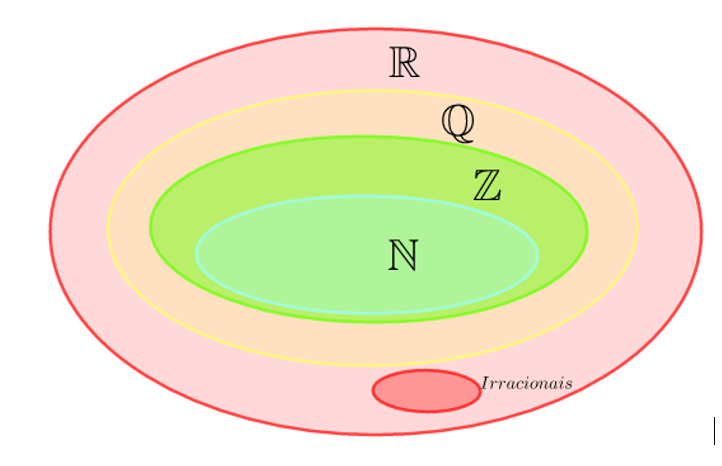
Observe o diagrama.
Na ordem temos as representações dos conjuntos: reais, racionais, inteiros, naturais e irracionais. Nele você conclui que todos os números que você conhece são números reais, mas nem todos é racional, inteiro ou natural.
Para finalizarmos esta atividade, preparei dois vídeos para explicar melhor sobre os números racionais e irracionais.
Ficamos por aqui, espero que você tenha aproveitado a atividade. Abraços e até a próxima.
| Objetivos de Aprendizagem e Desenvolvimento | Necessidade dos números reais para medir qualquer segmento de reta: – Medidas de diagonais de um polígono e alturas de um triângulo – Números racionais e irracionais: reconhecimento e localização de alguns na reta numérica: Números RacionaisNúmeros Irracionais (EAJAMA0802) Reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica (dízima periódica) e que pode ser escrita em forma de fração irredutível a/b, com b diferente de zero, localizando-os na reta numérica. (EAJAMA0803) Reconhecer um número irracional como um número real, cuja representação decimal é infinita |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).
