Olá, educando (a)! Esta videoaula de Matemática para a 6ª série da Eaja – foi veiculada na TV no dia 17/03/2021 (quarta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade você irá aprender como determinar os múltiplos e divisores de um número natural, a resolver problemas do cotidiano e perceber a importância desse estudo em nosso nosso dia-a-dia!

E aí, preparado?!
Então assista a videoaula a seguir, com a temática: problemas com múltiplos e divisores de um número natural
Olá, você sabe me responder se 354 é divisível por 2, por 3, por 5 ou por 6? Não! Espero que você queira saber. Então não deixe de ir até o final dessa atividade. Nela você irá aprender isso tudo e ainda conseguir resolver alguns problemas interessantes sobre esse tema da matemática.
Matemática no Cotidiano
Para introduzir o conteúdo de hoje, vou começar com um problema, eu mesmo vou resolver pra você.
Problema 1:
Suponha que você queira organizar um evento e encomendou 200 rosas, 150 margaridas e 75 cravos. Você quer fazer arranjos de flores para enfeitar o salão de festas, sem deixar sobrar nenhuma flor. Todos os arranjos devem ser iguais e, para isso, devem ter o mesmo número de rosas, de margaridas e também de cravos. Desejando montar o maior número possível de arranjos, quantas flores você deve colocar em cada um?
Complicado não é mesmo? Se escolhêssemos 15 arranjos e fossemos colocando 1 flor de cada tipo nos arranjos, ficaríamos horas e horas para organizar e ainda não saberíamos se iria sobrar alguma flor. Para facilitar a sua vida, a matemática vai te ajudar. Utilizaremos os conteúdos: divisores de um número e o máximo divisor comum.
Mas o que significa isso professor?
Uma definição bem simples, DIVISORES de um número natural são aqueles números que ao dividir o número dado, deixa resto zero.
E Máximo Divisor Comum é o maior divisor comum entre dois ou mais números.
Bom, partindo dessa definição, vamos resolver o problema.
Pense, quais são os números em que podemos dividir o 200, 150 e 75. Lembrando que quando um número divide outro deixa resto igual a zero.
Pensando, pensando, teremos:
D (200) = {1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100 e 200}
D (150) = {1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, e 150}
D (75) = {1, 3, 5, 15, 25 e 75}
Observe que o maior divisor comum entre os números 200, 150 e 75 é o 25, esse valor será o maior número de arranjos que você deve ter no seu evento.
Agora para encontrar o número de flores que deve ter cada arranjo, temos que dividir esses números por 25.
Dividindo o 200 por 25 obtemos 8, dividindo o 150 por 25 obtemos 6 e dividindo o 75 por 25 obtemos 3, somando esses três resultados, obtemos 17 flores em cada arranjo.
Achou complicado? ??
É só praticar um pouco que você irá conseguir fixar esse conteúdo.
Antes de partir para o próximo problema, acesse o vídeo no canal do Prof. Hélio para você entender melhor como determinar os divisores de um número e o máximo divisor comum.
Problema 2:
Suponha que você e seu amigo trabalham em uma confecção de calças e você folga a cada 6 dias e seu amigo folga a cada 8 dias. Vocês pretendem organizar uma festinha e precisava saber daqui a quantos dias vocês irão folgar juntos, se vocês folgaram hoje, para realizar a festa.
Para resolver este problema você poderia ir contando de 6 em 6 e de 8 em 8 até conseguir se encontrar, mas tem um assunto em matemática chamado de MÚLTIPLOS de um número e Mínimo Múltiplo Comum.
Antes de resolver o problema vamos definir.
Os múltiplos de um número são os números obtidos pela multiplicação desse número por um fator, que pode ser todos os números inteiros e o mínimo múltiplo comum MMC é o menor múltiplo, diferente de zero, entre dois ou mais números.
Então para resolver o problema basta encontrar o MMC. Seguindo:
M (6) = {0, 6, 12, 18, 24, 30, 36, 42, 48, …}
M (8) = {0, 8, 16, 24, 32, 40, 48, …}
Observando, notamos que o menor múltiplo comum, diferente de zero, entre o 6 e 8 é o 24, portanto os dois amigos podem organizar a festa daqui a 24 dias. Olha como ficou fácil resolver o problema utilizando o conteúdo matemático.
Preparei um vídeo para você entender melhor como determinar os múltiplos e o MMC.
Vamos comigo!!
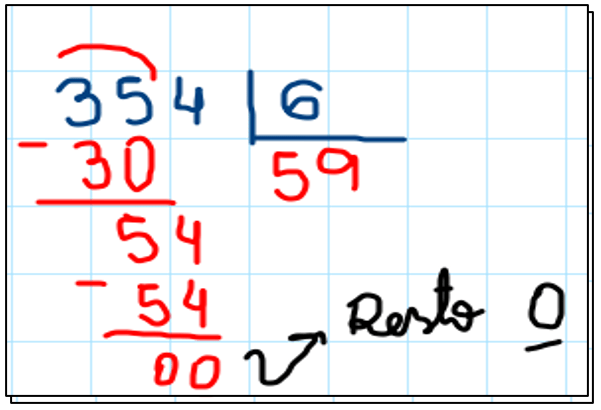
Antes de finalizar essa atividade vou resolver para você a questão proposta no início. Foi perguntado se você saberia dizer se 354 é divisível por 2, 3, 5 ou 6. Pela teoria estudada, 354 é divisível por 2, 3, e 6, pois ao realizar as divisões obtemos resto igual a zero. Não é divisível por 5 pois ao realizar a divisão, o resto não é igual a zero.
Observe a continha na figura abaixo.
Para finalizar, vou deixar 2 atividades para você tentar resolver, uma de MMC e outra de MDC
Atividade 1:
Eu observei na AV. Castelo Branco que um semáforo fica verde de 30 em 30 segundos e outro de 35 em 35 segundos. Supondo que eles ficaram verdes às 13h, eu preciso saber daqui a quantos segundos os dois ficarão verdes, juntos, novamente?
A dica aqui é determinar os múltiplos de 30 e de 35 e a resposta será o MMC entre eles. Veja:
M (30) = {0, 30, 60, 90, 120, 150, 180, 210, 240, …}
M (35) = {0, 35, 70, 105, 140, 175, 210, 245, …
Observa que o MMC de 30 e 35, diferente de zero, é o 210, logo podemos dizer que ficaram verdes, juntos, novamente será daqui a 210 segundos. Fica para você responder quantos minutos representa essa medida.
Atividade 2:
Você foi contratado para construir uma sala de eventos, ela terá três setores para acomodar o público. No setor A, de frente para o palco, terá 135 lugares, o setor B, na lateral direita, 105 lugares e o setor C, à esquerda, terá 90 lugares. O número de poltronas por fileiras será o mesmo nos três setores e o maior possível. Agora você deverá calcular quantas fileiras e quantas poltronas haverá em cada setor.
Ficamos por aqui, até a próxima.
| Objetivos de Aprendizagem e Desenvolvimento | Múltiplos e divisores de um número natural: ● Múltiplos ● Mínimo Múltiplo Comum ● Divisores ● Máximo Divisor Comum (EAJAMA0601) Resolver e elaborar situações-problema com números naturais, envolvendo as noções de divisor e de múltiplo, incluindo os conceitos de máximo divisor comum ou mínimo múltiplo comum. |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).
