ESTA PROPOSTA DE ATIVIDADE DE MATEMÁTICA, INTEGRADA COM ARTE, É DESTINADA AOS ESTUDADES DO 2º PERÍODO (3ª SÉRIE) DA EDUCAÇÃO DE JOVENS E ADULTOS – EJA.
NOÇÃO DE CONTAGEM SIMPLES
NO NOSSO DIA A DIA, FAZEMOS MUITAS ESCOLHAS QUE PODEM SER COMBINADAS DE DIFERENTES MANEIRAS. MAS QUANTAS COMBINAÇÕES PODEM SER FORMADAS? VAMOS ENTENDER ISSO MELHOR COM ALGUNS EXEMPLOS DO COTIDIANO.
QUANTAS REFEIÇÕES?
NO RESTAURANTE, O CLIENTE PODE MONTAR A SUA REFEIÇÃO ESCOLHENDO UM PRATO PRINCIPAL E UMA SALADA. AS OPÇÕES SÃO:
- 3 TIPOS DE PRATO PRINCIPAL (FEIJOADA, FILÉ COM FRITAS E STROGONOFF).
- 2 TIPOS DE SALADA (TROPICAL E REPOLHO).
QUANTAS REFEIÇÕES PODEM SER FORMADAS COM ESSAS OPÇÕES?
NESTE PROBLEMA, PRECISA CONTAR QUANTAS COMBINAÇÕES DE PRATO PRINCIPAL E SALADA SÃO POSSÍVEIS COM AS QUANTIDADES APRESENTADAS.
VEJAMOS AS POSSIBILIDADES.

A QUANTIDADE TOTAL DE COMBINAÇÕES É RESULTADO DA MULTIPLICAÇÃO DA QUANTIDADE DE PRATOS PRINCIPAIS PELA QUANTIDADE DE SALADAS:
3 X 2 = 6
É O QUE CHAMAMOS DE RACIOCÍNIO COMBINATÓRIO CUJA OPERAÇÃO É A MULTIPLICAÇÃO.
BOM ESTUDO.
QUESTÃO 1
NATÁLIA FAZ BOLOS POR ENCOMENDA. VEJA AS OPÇÕES QUE NATÁLIA OFERECE.

O CLIENTE MONTA O BOLO ESCOLHENDO UM TIPO DE MASSA, UM RECHEIO TRADICIONAL E UM RECHEIO ESPECIAL. O NÚMERO DE COMBINAÇÕES POSSÍVEIS PARA MONTAR O BOLO É IGUAL A
(A) 9.
(B) 18.
(C) 23.
(D) 24.
QUESTÃO 2
JOSÉ ESTÁ PLANEJANDO VISITAR SEUS FAMILIARES EM ORIXIMINÁ, NO ESTADO DO PARÁ. A VIAGEM SERÁ FEITA EM DUAS PARTES:
- A PRIMEIRA DE GOIÂNIA A SANTARÉM, NO PARÁ;
- A SEGUNDA, DE SANTARÉM A ORIXIMINÁ.
DE GOIÂNIA A SANTARÉM, JOSÉ TERÁ TRÊS OPÇÕES DE TRANSPORTE: AVIÃO, CARRO OU ÔNIBUS. DE SANTARÉM A ORIXIMINÁ, JOSÉ TERÁ 2 OPÇÕES DE BARCO.
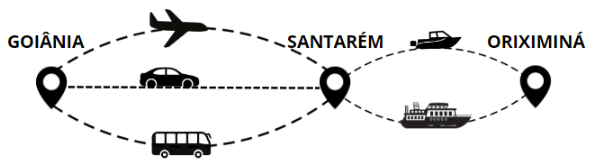
COMBINANDO UMA OPÇÃO DE TRANSPORTE PARA CADA ETAPA, O TOTAL DE OPÇÕES QUE JOSÉ TEM PARA SAIR DE GOIÂNIA E CHEGAR A ORIXIMINÁ É IGUAL A
(A) 6.
(B) 4.
(C) 3.
(D) 2.
QUESTÃO 3
ÂNGELA ADOTOU A IDEIA DE TER POUCAS PEÇAS DE ROUPAS QUE POSSAM SER COMBINADAS E ASSIM ELA PODE SE VESTIR DE VÁRIAS FORMAS. ÂNGELA COMPROU 5 BLUSAS E 3 CALÇAS. COMBINANDO UMA BLUSA E UMA CALÇA, DE QUANTAS FORMAS DIFERENTES ÂNGELA PODE SER VESTIR COM ESSAS PEÇAS?
QUESTÃO 4
OBSERVE ESSA IMAGEM COM ATENÇÃO.

AS CORES, O TEXTO, A IMAGEM DO CAFÉ QUENTINHO SENDO COLOCADO NA XÍCARA CHAMAM A ATENÇÃO E PODEM DESPERTAR MEMÓRIAS OU OUTROS SENTIDOS PARA ALÉM DA VISÃO.
AGORA RESPONDA:
A) QUAL É A MENSAGEM PRINCIPAL DA IMAGEM?
B) QUAIS DOS SEUS SENTIDOS ESSA IMAGEM DESPERTA?
| AUTORIA | CRISTIANE SOARES DE SOUZA, LICENCIATURA EM MATEMÁTICA. |
| COMPONENTES CURRICULARES | MATEMÁTICA E ARTE. |
| OBJETIVOS DE APRENDIZAGEM E DESENVOLVIMENTO | (EJAMA0235) Ler, analisar e interpretar, com mediação do professor, tabelas e gráficos simples. (EJAAV0201) Conhecer e investigar elementos da arte visual que dialogue com outros sentidos além do visual: audição, tato, paladar, explorando suas diferentes percepções e significados. |
| REFERÊNCIAS | TEIXEIRA, Paulo Jorge Magalhães. Práticas pedagógicas envolvendo o raciocínio combinatório desde os anos iniciais do ensino fundamental. UFF. URL https://www1.sinprosp.org.br/congresso_matematica/revendo/dados/files/textos/Sessoes/PR%C3%81TICAS%20PEDAG%C3%93GICAS%20ENVOLVENDO%20O%20RACIOC%C3%8DNIO%20COMBINAT%C3%93RIO%20DE.pdf, consultado em 02/07/24. Glória, C. M., Nunes, M. V., & Moraes, G. M. (2021). RACIOCÍNIO COMBINATÓRIO NOS ANOS INICIAIS DE ESCOLARIZAÇÃO: uma abordagem com materiais didáticos alternativos . Ensino Da Matemática Em Debate, 8(2), 92–116. URL https://doi.org/10.23925/2358-4122.2021v8i2p92-116 |

