Esta proposta de atividade de Matemática é destinada aos estudantes do 4º Período da Educação de Jovens e Adultos – EJA.
Introdução
As expressões numéricas com frações envolvem números racionais e operações matemáticas básicas organizadas em uma sequência que deve ser respeitada. Vamos explorar como resolver essas expressões com segurança e entender algumas dicas úteis!
Imagem produzida no canva.com/
Os números racionais (Só para Lembrar!)
Números racionais são aqueles que podem ser representados na forma de fração
a/b , onde a e b são números inteiros e b ≠0.
Exemplos:
3/7 , -5/2 , 8=8/1 e 0=0/1
Por que Entender Operações com Sinais é Importante?
Resolver expressões numéricas corretamente exige atenção aos sinais, pois eles definem o comportamento do resultado das operações. Vale guardar, ou compreender a regra dos sinais para evitar erros no cálculo final.
Regra dos Sinais
Na multiplicação ou divisão:
- Sinais iguais: o resultado é positivo.
- Sinais diferentes: o resultado é negativo.
Na Adição ou subtração:
- Sinais iguais: soma e conserva o sinal.
- Sinais diferentes: subtrai e conserva o sinal do maior (em módulo).
Macete para Resolver Expressões
- Respeite a ordem das operações:
- Resolva primeiro os parênteses, depois colchetes e, por último, as chaves.
- Em seguida, calcule potências, depois multiplicações e divisões (na ordem em que aparecem) e, por fim, adições e subtrações.
- Simplifique frações sempre que possível.
- Para adição ou subtração, reduza as frações ao mesmo denominador, ou faça os cálculos de forma simplificada (veja no exemplo).
- Realize as operações uma a uma, com calma, seguindo a sequência correta.
Exemplos para Praticar
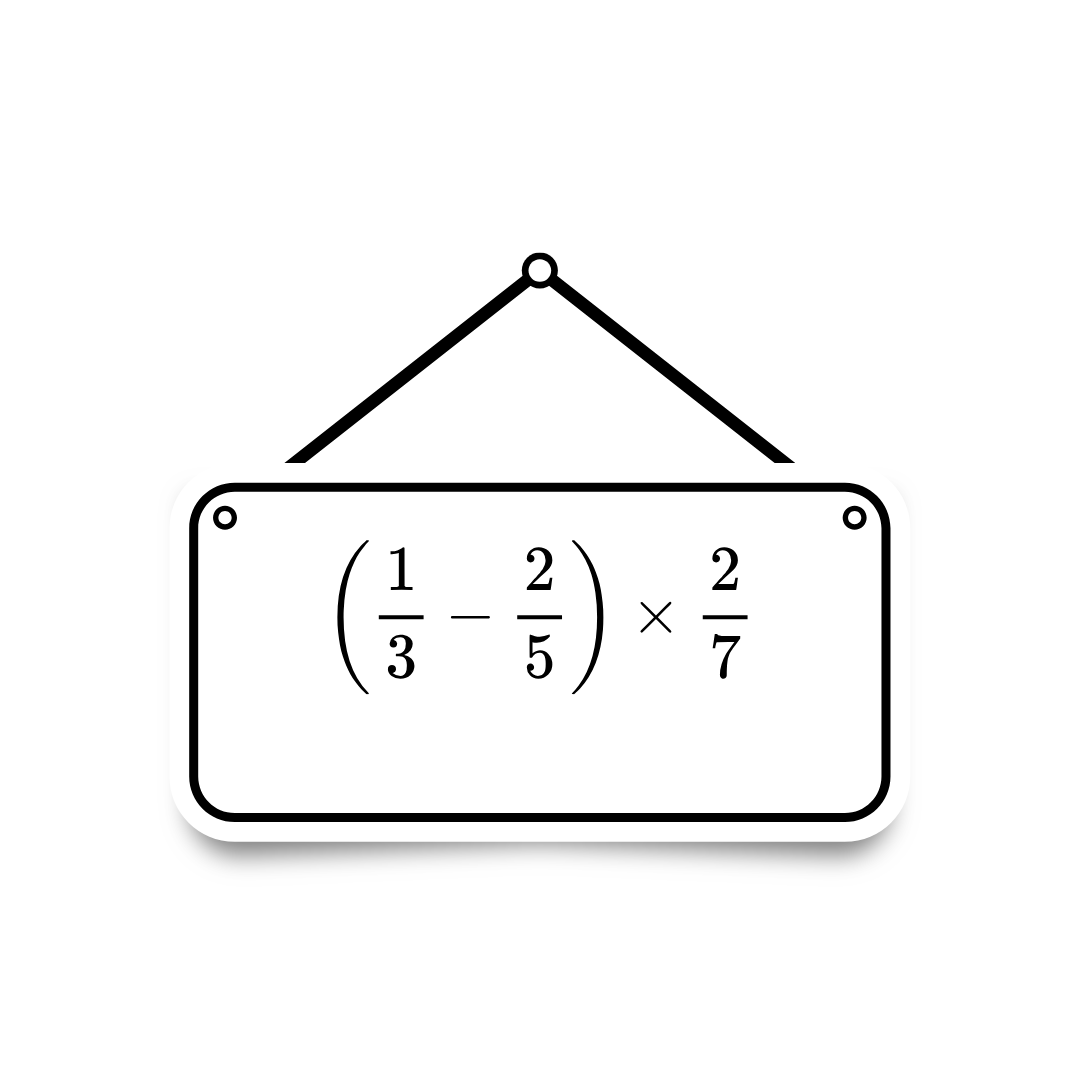
Exemplo 1:
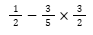
Primeiro a Multiplicação.
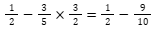
Agora a Subtração (Vamos resolver através de um macete).

Finalizando.
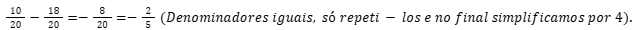
Exemplo 2:
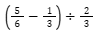
Primeiro a subtração dentro dos parênteses utilizando o macete.
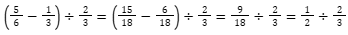
Aqui, simplificamos por 9 a fração 9/18.
Agora a divisão (Lembre-se que é a operação inversa da multiplicação).
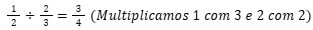
Exemplo 3:
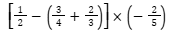
Resolvendo a adição dentro dos parênteses utilizando o macete.
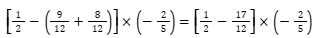
Resolvendo a subtração dentro dos colchetes utilizando o macete.
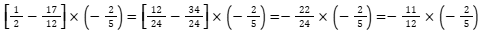
Aqui, simplificamos a fração 22/24 por 2.
Finalizando com a multiplicação e lembrando da regra dos sinais.
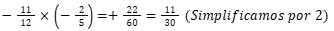
Dica Final
Dominar as expressões numéricas com frações pode parecer um desafio no início, mas com prática e atenção aos sinais e à ordem das operações, você estará pronto para resolver qualquer problema com confiança!
Ficamos por aqui, até o próximo.
QUESTÃO 01
Nas expressões numéricas com frações, a ordem das operações deve ser respeitada. Primeiramente, resolvem-se as operações que estão
(A) fora dos parênteses, colchetes e chaves.
(B) dentro dos parênteses, depois colchetes e, por fim, chaves.
(C) nos colchetes, antes dos parênteses.
(D) somente fora dos parênteses e colchetes.
QUESTÃO 02
A regra do sinal estabelece que o resultado de uma multiplicação ou uma divisão entre dois números com sinais iguais será sempre
(A) negativo.
(B) neutro.
(C) positivo.
(D) indefinido.
QUESTÃO 03
Resolva a seguinte expressão numérica com frações:

Explique os passos seguidos para encontrar o resultado final.
QUESTÃO 04
Simplifique a seguinte expressão numérica:
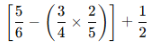
Mostre detalhadamente cada etapa da resolução.
SAIBA MAIS
Aprenda um pouco mais no canal do Prof. Hélio
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0415) Interpretar e resolver situações-problema que envolvam cálculos com números racionais, com compreensão dos processos neles envolvidos. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9° ano – Ensino Fundamental; Matemática; Goiânia,2024. |