Matemática – Critérios de divisibilidade

Esta proposta de atividade de Matemática é destinada aos estudantes do 4º Período (5ª série) da Educação de Jovens e Adultos – EJA.

Critérios de Divisibilidade

Por exemplo: 

Paulo tem 3 filhos e precisa repartir, em quantidades iguais e inteiras, uma herança de 63987 reais. Será que essa divisão seria possível?

Você poderá resolver essa divisão utilizando uma calculadora, mas se não tiver?

Sabendo o critério de divisibilidade por 3, com certeza sua resposta será sim.

Só para lembrar:

Um número será divisível por outro quando o resto da divisão entre eles for igual a zero.

Vou apresentar alguns critérios de divisibilidade, outros você pode acessar os slides no link BAIXE SLIDES.

1º) Critério de divisibilidade por 2.

O número natural deve ser PAR, ou seja, terminar em 0, 2, 4, 6 ou 8.

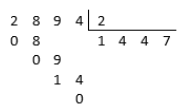
Exemplo: 2894 (Número par terminado em 4).

Observe a divisão e veja que o resto é igual a zero.

2º) Critério de divisibilidade por 3.

A soma de todos os algarismos no número natural deve ser um número múltiplo de 3 (divisível por 3).

Exemplo: 7524

Soma dos algarismos = 7+5+2+4 = 18 (18 é divisível por 3).

Veja que o resto, na divisão, é igual a zero.

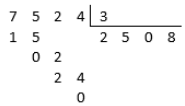
3º) Divisibilidade por 5.

O número natural deve terminar em 0 (zero) ou 5.

Exemplos: 1260 e 3245 

Veja que nas divisões o resto deu zero.

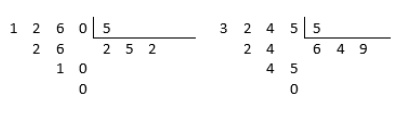
4º) Divisibilidade por 9.

Semelhante ao critério do 3, neste caso a soma dos algarismos do número natural deve ser um número múltiplo de 9 (divisível por 9).

Exemplo: 9738

Soma dos algarismos = 9+7+3+8=27 (27 é divisível por 9).

Veja a divisão com resto zero.

5º) Divisibilidade por 10, 100 e 1000.

Um número natural será divisível por 10, 100 ou 1000 se terminar, respectivamente, em 0, 00 ou 000.

Exemplo:

a) 250 divide por 10 pois termina em 0 (zero).

b) 1300 divide por 100 pois termina em 00.

c) 71000 divide por 1000 pois termina em 000.

Agora vamos para a atividade.

Questão 01

O Sr. João precisa dividir uma herança de R $98396,00 entre seus 9 filhos, só que a divisão deverá ser inteira. Seu filho, Paulo, disse que essa divisão é possível pois aprendeu, na escola, o critério de divisibilidade por 9. 

E você, acha que é possível? Justifique sua resposta utilizando o critério e realizando a divisão.

Questão 02

De acordo com os critérios de divisibilidade, podemos afirmar que

(A) um número será divisível por 3 se ele for ímpar.

(B) um número será divisível por 4 se terminar em 00.

(C) um número será divisível por 5 se ele terminar somente em 5.

(D) um número será divisível por 6 se ele for par.

Questão 03

A costureira Paula recebeu uma encomenda para fazer algumas faixas. Para realizar o serviço, ela precisa dividir um rolo de 876 metros de fita em 3 partes iguais. De imediato, pegou a calculadora para realizar a divisão, porém, lembrou da última aula de matemática e concluiu que a divisão seria um número exato. 

A) Paula está certa? 

B) Justifique sua resposta utilizando o critério de divisibilidade por 3 e realizando a divisão.

Questão 04

Aplicando os critérios de divisibilidade, podemos afirmar que

(A) 483 é divisível por 2.

(B) 896 é divisível por 3.

(C) 234 é divisível por 4.

(D) 230 é divisível por 100.

Saiba mais

Assista aos vídeos no canal do Prof. Hélio para saber um pouco mais sobre os critérios de divisibilidade.

Autoria	Hélio Roberto da Rocha, Mestre em Matemática
Componente Curricular	Matemática
Objetivos de aprendizagem e desenvolvimento	(EJAMA0409) Compreender e aplicar os critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100 e 1000.
Referências	SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018.PATARO, Patricia Moreno Matemática essencial 6° ano: ensino fundamental, anos finais / Patricia Moreno Pataro, Rodrigo Balestri. – 1. ed. – São Paulo: Scipione, 2018.