Olá! Esta aula de Matemática é destinada aos educandos da 8ª Série da Eaja.
Nesta aula você estudará sobre os números irracionais, como reconhecê-los e resolverá algumas situações problema.
ASSISTA À VIDEOAULA A SEGUIR COM A TEMÁTICA NÚMEROS IRRACIONAIS.
Como você assistiu na videoaula do professor Hélio Rocha, o tema da aula de hoje não é muito utilizado nos nossos afazeres do dia-a-dia, mas tem a sua importância. Quer ver só? Você não costuma ver nos supermercados valores de produtos representados por um radical. Seria um absurdo representar o preço de um litro de leite por R$√19,00, mas nos cálculos para determinar o número de polegadas de uma TV, você encontra um valor representado por uma raiz.
Relembrando o conceito de Raiz na linguagem matemática.
Raiz
Sejam a e b dois números reais e n um número natural diferente de zero, então:
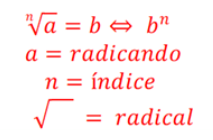
Achou complicado essa definição? Veja alguns exemplos:
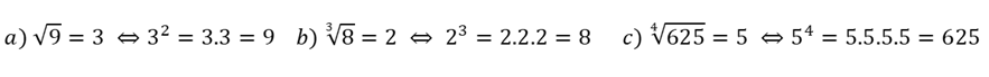
Introdução do conceito de números irracionais
Os números irracionais são todos aqueles números que não podem ser escritos na forma de a/b (fração), em que a e b são número inteiros com b diferente de zero. Quando representado na forma decimal, os números irracionais possuem infinitas casas decimais e não periódicas.
Observe alguns exemplos de números irracionais.
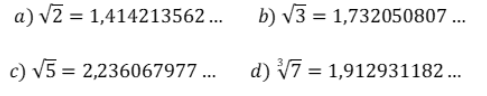
Na situação problema a seguir você verificará a aplicabilidade dos números irracionais.
Situação Problema 01 – Explicação
Hélio ficou curioso para verificar se o número de polegadas de sua TV, 50 polegadas, estava correto. Então, ele fez as medidas do comprimento e da largura da TV e obteve, respectivamente, 110cm e 62cm. E em seguida fez os cálculos.
Mas como ele fez esses cálculos?
Utilizou o Teorema de Pitágoras (a medida da hipotenusa é igual a raiz quadrada da soma dos quadrados dos catetos).
A medida da hipotenusa representa a medida da diagonal da tela da TV e os catetos o comprimento e a largura. Fazendo os cálculos obtemos.
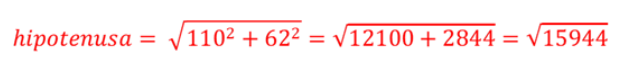
Para calcular o valor dessa raiz, você precisa determinar um número que elevado ao quadrado, ou seja, multiplicar ele duas vezes, Neste caso você obterá 15944. Utilizando uma calculadora, fica fácil obter.
Hipotenusa = 126,2695529413167756939643208567…cm. Esse número iremos aproximar para 126,27cm.
Para determinar o número de polegadas, é preciso lembrar que uma polegada possui, aproximadamente, 2,56cm
Logo as polegadas dessa TV será igual a 126,27:2,56=49,32 polegadas. Aproximamos para 50 polegadas.
Hélio então confirmou que sua TV tem realmente, de 50 polegadas.
Na situação problema 01, ao determinarmos a raiz quadrada da hipotenusa, obtivemos um número irracional. Podemos então concluir que todo número que não possui raiz exata é um número irracional, sua parte decimal é infinita e não periódica. Um número irracional bastante conhecido é o número ϖ (letra grega pi), que é o valor da razão entre o comprimento e o diâmetro de uma circunferência.
Exemplo envolvendo o número pi
Realizando as medições do comprimento da circunferência e do diâmetro de um objeto na forma de um cilindro, por exemplo uma lata de leite em pó, chegamos às medidas, respectivamente, 49,9 cm e 15,8 cm. Vamos verificar o valor do pi.
Pi = 49,9 : 15,8 = 3,1582278481012658227848101265823…
Esse valor é o valor próximo do pi.
Atenção!! Utilizando calculadoras científicas e programas de computador específico, obtemos o valor do pi com várias casas decimais.
Pi = 3,1415926535897932384626433832795028841…
Quer saber um pouco mais sobre o número Pi, então assista ao vídeo no canal do professor Hélio Rocha, clicando no link: https://www.youtube.com/watch?v=oR-UlHY_p6w
Atividade 1
Faça as medições da largura e do comprimento de sua TV, realize os cálculos, seguindo o modelo, e verifique se sua TV possui o número de polegadas informado pelo fabricante.
Atividade 2
Faça as medições do comprimento e do diâmetro da circunferência de objetos, como latas de refrigerantes, latas de leite em pó, entre outros, na forma de cilindro. Após realizar as medições, divida a medida do comprimento pelo diâmetro, você irá chegar a valores próximos do valor do Pi.
Atividade 3
Das raízes quadradas a seguir, encontre aquela que corresponde a um número irracional. Utilize uma calculadora.

Atividade 4
Dos números a seguir, podemos afirmar que todos são irracionais, exceto:
- 8,1011121314152034….
- Raiz quadrada de 3
- Raiz quadrada de 5
- 3,141592
- pi
Atividade 5
Resolva a expressão abaixo e verifique se o resultado é um número irracional. Justifique sua resposta.
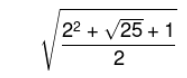
Finalizamos nossa aula de hoje. Até a próxima ! Abraços!
| Referência | Sousa, Joamir Roberto de – Matemática realidade & tecnologia: 9º ano |
| Componente Curricular | Objetivo de aprendizagem e desenvolvimento |
| Matemática | (EAJAMA0803) Reconhecer um número irracional como um número real, cuja representação decimal é infinita |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).

