Olá! Esta aula de Matemática é destinada aos educandos da 6ª Série da Eaja.
Nesta aula você aprenderá Múltiplos e Mínimo Múltiplo Comum e resolverá algumas situações-problema utilizando esses conceitos.
Assista à videoaula do professor Hélio Rocha com a temática Múltiplos e Mínimo Múltiplo Comum (MMC)
Múltiplo de um Número Natural : dizemos que um número é múltiplo de outro, se o primeiro é resultado da multiplicação do segundo por um número natural qualquer. Veja os exemplos:
8 é múltiplo de 4, pois 8 = 4 x 2
36 é múltiplo de 9, pois 36 = 9 x 4
Pode-se utilizar a divisão para verificar se um número é múltiplo de um número natural.
Exemplo
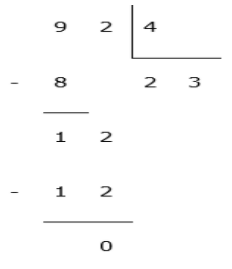
Como a divisão de 92 por 4 é exata, podemos afirmar que:
92 é múltiplo de 4, pois 4.23=92;
92 é múltiplo de 23, pois 23.4 = 92
Situação Problema 1 – Explicação
Esse problema foi aplicado na avaliação do Enem-2014.
Uma loja decide premiar seus clientes. Cada cliente receberá um dos seis possíveis brindes disponíveis, conforme sua ordem de chegada na loja. Os brindes a serem distribuídos são: uma bola, um chaveiro, uma caneta, um refrigerante, um sorvete e um CD, nessa ordem. O primeiro cliente da loja recebe uma bola, o segundo um chaveiro, o terceiro uma caneta, o quarto um refrigerante, o quinto um sorvete, o oitavo um chaveiro, e assim sucessivamente, segundo a ordem dos brindes. Qual será o brinde que irá receber o milésimo cliente.
E agora, como solucionar esse problema? Contando até 1000 e marcando o prêmio? Seria muito trabalhoso. Veja como fazer a divisão entre 1000 pessoas por 6 brindes e ver o resto.
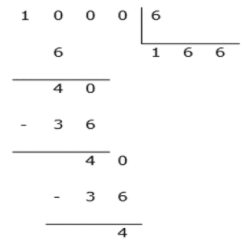
E aí, o que você percebe? Já sabe a resposta? Veja a explicação:
- Enumerando os brindes: 1 = bola, 2 = chaveiro, 3 = caneta, 4 = refrigerantes, 5 = sorvete e 6 = CD.
- Como o resto obtido foi igual a 4 e o número 4 representa REFRIGERANTE, podemos afirmar que o milésimo cliente receberá um refrigerante.
Atividade 1
Utilizando a técnica da flipagem (mover rapidamente), quantos desenhos são necessários para se produzir um filme de animação de 40 segundos em que, para cada segundo, há 12 desenhos? O número correspondente à quantidade de desenhos que você obteve como resposta é múltiplo de 12? Explique.
Você viu o que são números Múltiplos. Agora, vamos para o próximo assunto dessa aula, o Mínimo Múltiplo Comum (MMC).
Mínimo Múltiplo Comum (MMC): o mínimo múltiplo comum entre dois ou mais números é o menor número diferente de zero, que é múltiplo comum desses números.
Lembre-se! Só tem sentido falar de MMC de dois ou mais números.
Exemplo
Qual o MMC entre 6 e 8?
Vamos determinar os múltiplos de 6 e 8
M(6)= {0,6,12,18,24,30,36,…}
M(8)={0,8,16,24,32,40,…}
O MMC, diferente de zero, entre 6 e 8 é o número 24.
Situação Problema 2 – Explicação
Suponha que você trabalha em um supermercado e que o seu patrão lhe peça para empilhar caixas cúbicas de dois tipos: caixa com 12 cm de altura e caixas com 20 cm de altura. Precisa saber quantos centímetros de altura devem ter esses empilhamentos, no mínimo, de maneira que ambos fiquem no mesmo nível?
Para resolver esse problema, você poderia optar em ir empilhando lado a lado as caixas até conseguir que as colunas fiquem na mesma altura, mas poderá optar em determinar o MMC entre 12 e 20, o mais fácil.
Podemos optar em determinar, separadamente, os múltiplos de 12 e 20 e depois observar o menor comum entre eles.
Para determinar os múltiplos, basta ir multiplicando 12 e 20 pelos números naturais: 0, 1, 2, 3, 4, 5, 6, 7, … até você encontrar um múltiplo comum, diferente de zero.
M(12)= {0, 12, 24, 36, 48, 60, 72, …}
M(60)= {0, 60, 120, 180,…}
Logo o MMC(12,20)= 60 e os empilhamentos de caixas devem ter, no mínimo, 60cm de altura.
Atividade 2
1) Calcule o MMC números abaixo.
a) 18 e 60
b) 210 e 462
2) Observe os números abaixo e responda às questões.
10 21 22 45 72 140 63 121 91 18 7
Quais desses números são:
- Múltiplos de 9?
- Múltiplos de 5?
- Múltiplos de 27
- Simultaneamente múltiplos de 2 e de 9?
3) (Fuvest – SP) No alto da torre de uma emissora de televisão, duas luzes “piscam” com frequências diferentes. A primeira “pisca” 15 vezes por minuto e a segunda “pisca” 10 vezes por minuto. Se num certo instante, as luzes piscam simultaneamente, após quantos segundos elas voltarão a “piscar simultaneamente”?
Chegamos ao final de mais uma aula. Abraços e até a próxima!
| Referência | Sousa, Joamir Roberto de – Matemática realidade & tecnologia: 6º ano. |
| Componente Curricular | Habilidade |
| Matemática | (EAJAMA0601) Resolver e elaborar situações-problema com números naturais, envolvendo as noções de múltiplo, incluindo os conceitos de mínimo múltiplo comum (ADAPTADA). |

