Esta proposta de atividade de matemática é destinada aos estudantes do 3º ano do Ensino Fundamental.

Malhas quadriculadas e figuras congruentes
Hoje vamos descobrir algo muito legal: como desenhar figuras em malhas quadriculadas ou triangulares e reconhecer quando duas figuras são iguais, mesmo que estejam em lugares diferentes. Parece mágico, mas na verdade é matemática!
Você já brincou de montar peças iguais, como blocos de construção ou quebra-cabeças? Quando duas peças têm a mesma forma e o mesmo tamanho, dizemos que elas são congruentes. A palavra é grande, mas o significado é simples: congruente quer dizer igualzinho!
Agora vamos usar as malhas quadriculadas (cheias de quadradinhos) ou malhas triangulares (cheias de triângulos) para desenhar. Elas funcionam como um mapa que nos ajuda a fazer os desenhos com mais precisão. Se eu desenhar um coração em 2 quadradinhos de largura e 2 de altura, e você desenhar outro igual, mesmo que esteja em outro lugar da malha, eles serão figuras congruentes!

Também podemos sobrepor as figuras — ou seja, colocar uma em cima da outra. Se elas se encaixarem direitinho, quer dizer que são congruentes. Podemos fazer isso com papel vegetal, com transparência ou até com o computador e tablet usando aplicativos de desenho. Para esta atividade, utilizei o Canva (www.canva.com) e as formas geométricas disponíveis no Word da Microsoft.
ASSISTA A VIDEOAULA SOBRE ESSE CONTEÚDO:
RESPONDA ÀS QUESTÕES:
QUESTÃO 1
Quando duas figuras têm a mesma forma e o mesmo tamanho, mesmo que estejam em posições diferentes, elas são chamadas de
(A) semelhantes.
(B) congruentes.
(C) diferentes.
(D) sobrepostas.
QUESTÃO 2
Uma maneira de verificar se duas figuras desenhadas em uma malha são congruentes é
A) contar quantos lápis foram usados para desenhar.
B) comparar a cor e o tamanho de cada uma das figuras.
C) sobrepor uma figura sobre a outra ou usar medidas da malha.
D) colocar as figuras em lugares diferentes e observar se mudam de forma.
QUESTÃO 3
Uma maneira de verificar se duas figuras desenhadas em uma malha são congruentes é
A) contar quantos lápis foram usados para desenhar.
B) comparar a cor e o tamanho de cada uma das figuras.
C) sobrepor uma figura sobre a outra ou usar medidas da malha.
D) colocar as figuras em lugares diferentes e observar se mudam de forma.
QUESTÃO 4
Desenhe cinco figuras diferentes em sua malha quadriculada (malha em anexo).
Agora desenhe cada figura novamente em outro lugar da malha, mudando a posição (vire, deslize ou gire).
Circule os pares de figuras que são iguais em forma e tamanho.
Pegue um papel vegetal ou transparência e tente sobrepor os pares para ver se elas se encaixam perfeitamente.
QUESTÃO 5
Desenhe uma figura em sua malha.
Crie um “caminho” de figuras congruentes, mudando apenas a posição ou orientação.
Conte para a turma como percebeu que todas as figuras eram iguais, mesmo mudando de lugar ou de direção.

QUESTÃO 6
Você quer fazer um mosaico na sua malha quadriculada usando quadrados, triângulos e retângulos. Para que o mosaico fique bonito e simétrico, você precisa que várias figuras sejam iguais em forma e tamanho.
Pergunta: Qual é a palavra que descreve essas figuras iguais, que podem estar em posições diferentes no mosaico?

QUESTÃO 7
Dê um belíssimo colorido para este mosaico e depois mostre-o aos colegas.
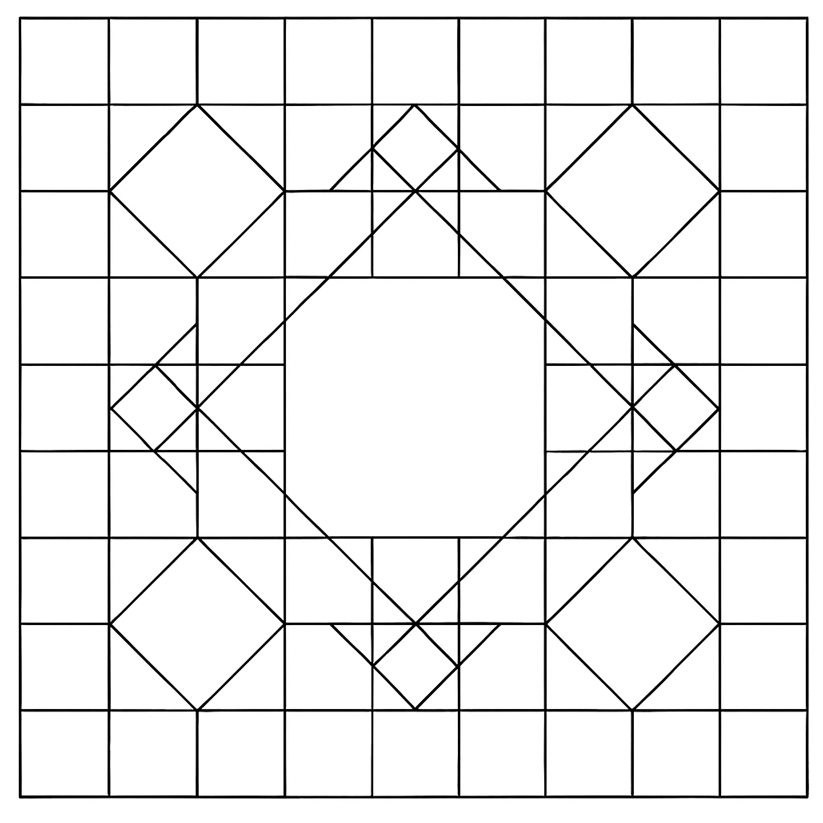
ANEXO

| Autoria: | Prof.ª Esp. Danielle Assis Borges |
| Formação: | Graduanda em Nutrição. Graduada em Jornalismo e Pedagogia. Pós-graduada em: – MBA em Gestão das Tecnologias da Informação e da Comunicação – Educação; – Docência Universitária; -Psicopedagogia Institucional e Clínica; – Neuropedagogia Aplicada à Educação. |
| Componente Curricular: | Matemática |
| Conteúdo(s)/objeto(s) de conhecimento: | Congruência de figuras planas; Desenhos em malhas quadriculadas ou triangulares de figuras planas |
| Descritor(es) SAEB: | — |
| Habilidade(s)/objetivo(s) de aprendizagem e desenvolvimento: | DOCUMENTO CURRICULAR PARA GOIÁS – AMPLIADO: (EF03MA16-B) Desenhar em malhas quadriculadas ou triangulares figuras planas em posições distintas, com a mesma forma e o mesmo tamanho. (EF03MA16-C) Reconhecer figuras congruentes, usando sobreposição e desenhos em malhas quadriculadas ou triangulares, incluindo o uso de tecnologias digitais, em situações diversas. |
| Referências: | BRASIL. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira – INEP. Sistema de Avaliação da Educação Básica – SAEB: resultados e metodologia. Brasília: INEP, 2023. Disponível em: https://www.gov.br/inep/pt-br/areas-de-atuacao/avaliacao-e-exames-educacionais/saeb. Acesso em: 29, set. 2025. CANVA. Ferramenta de design gráfico online. Disponível em: https://www.canva.com/. Acesso em: 29, set. 2025. DANTE, Luiz Roberto; VIANA, Fernando. Ápis mais: matemática: 3º ano. São Paulo: Ática, 2021. GOIÂNIA (Município). Secretaria Municipal de Educação. Matriz de habilidades para o Ensino Fundamental – 4º bimestre – 3º ano. Goiânia: Prefeitura de Goiânia, [2024]. Documento interno. GOIÁS. Secretaria de Estado da Educação. Documento Curricular para Goiás: ampliado – Etapa Ensino Fundamental: anos finais. Goiânia: Seduc, 2019. SOUZA, Joamir Roberto de; SOUZA, Maria Angélica Reghin de. Entrelaços: matemática: 3º ano fundamental: anos iniciais. 1. ed. São Paulo: FTD, 2021. |
