Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Regra de três composta
Em várias situações do dia-a-dia, é preciso analisar, comparar grandezas para tomar decisões, como por exemplo, quanto
- mais tempo demorar para arrumar uma torneira que está pingando, mais água vai vazar;
- mais estudantes no grupo de trabalho, menos tempo será gasto para terminar uma lista de exercícios;
- menos pessoas na lista de convidados, menos comida será necessária.
Essas grandezas têm uma relação de dependência que pode ser direta ou inversamente proporcional, chamada de razão de proporcionalidade.
Para resolver um problema que relaciona mais de duas grandezas, usamos o método da regra de três composta. Esta solução considera a razão de proporcionalidade entre as grandezas: se uma grandeza é proporcional a outras duas (ou mais), então é proporcional também ao produto entre essas duas (ou mais) grandezas.
Veja como isto se aplica nas situações a seguir.
Exemplo 1:
Um grupo com 3 estudantes precisam pintar um painel para a aula de Ciências. Eles têm 5 dias para concluir esta tarefa, por isso trabalharão por 2h por dia. Se o grupo aumentar para 4 estudantes e para 3h de trabalho por dia, em quanto tempo vão concluir a pintura do painel?
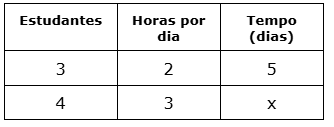
Comparando as grandezas:
- “Tempo para concluir o trabalho” com “número de estudantes no grupo” são grandezas inversamente proporcionais. Isto porque, mais estudantes no grupo farão o trabalho em menos tempo.
- “Tempo para concluir o trabalho” com “horas de trabalho por dia” também são grandezas inversamente proporcionais. Isto porque, menos dias para concluir a tarefa mais horas de trabalho diário serão necessárias.
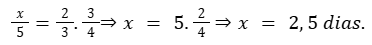
Veja que com 1 pessoa a mais no grupo e trabalhando 1 hora a mais por dia, o trabalho será concluído na metade do tempo previsto, ou seja, em 2,5 dias.
Exemplo 2:
Para fazer o lanche na escola, a cozinheira gasta 5kg de arroz para servir 2 refeições para 75 estudantes. Quantos kg de arroz serão necessários para servir 100 estudantes em 3 refeições?
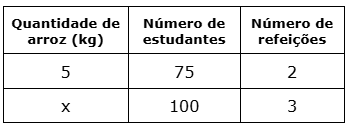
Comparando as grandezas:
- “Quantidade de arroz” com “número de estudantes” são grandezas diretamente proporcionais. Isto porque, mais arroz serve mais estudantes.
- “Quantidade de arroz” com “Número de refeições” também são grandezas diretamente proporcionais. Isto porque, mais arroz permite oferecer mais refeições.
Reveja esses conceitos na videoaula “Grandezas proporcionais” da professora Cristiane Souza, do Canal Estúdio Conexão Escola.
Aplique seus conhecimentos na resolução das atividades a seguir.
QUESTÃO 1
Na reforma da escola, estão trabalhando 4 pedreiros que cumprem uma jornada de 8 horas por dia e devem concluir a obra em 2 meses.
Matematicamente, a quantidade de pedreiros, a carga horária diária de trabalho e o tempo de duração da obra são grandezas que se relacionam. Comparando essas grandezas,
(A) quantidade de pedreiros e o tempo da obra são diretamente proporcionais.
(B) quantidade de pedreiros e o tempo da obra são inversamente proporcionais.
(C) carga horária de trabalho e o tempo da obra são diretamente proporcionais.
(D) carga horária de trabalho e o tempo de obra não são proporcionais.
QUESTÃO 2
Na turma do 9º ano há 35 estudantes. Em um dia que todos estão presentes, o grupo consome 18 litros de água em 4h de aula.
Hoje estão presentes 24 estudantes que permanecerão na escola por 5 horas. Quantos litros de água devem ser consumidos por esse grupo mantendo-se a mesma proporção?
QUESTÃO 3
O chuveiro elétrico é considerado o vilão da conta de energia. Por isso, Marcos decidiu fazer as contas e trocar o chuveiro por outro mais econômico e com a mesma eficiência.
Na casa dele, o chuveiro elétrico era de 4.500W de potência e consumia mensalmente, 67,5 kWh, o que representava R$57,38 da conta de energia. O novo chuveiro é de 3.500W de potência e representa R$ 44,65 da conta de energia elétrica. Qual é o consumo mensal do novo chuveiro?
QUESTÃO 4
Em uma fazenda foram colhidas 9 toneladas de milho usando 3 tratores, que trabalharam 6 horas por dia, durante 20 dias. Se fosse preciso colher a mesma quantidade de milho em apenas 10 dias, deveriam ser usados 5 tratores trabalhando
(A) 5 horas por dia.
(B) as mesmas 6 horas por dia.
(C) menos de 6 horas por dia.
(D) mais de 6 horas por dia.
QUESTÃO 5
Pense em uma situação do seu dia a dia (na escola, em casa, no esporte, no lazer ou em atividades da comunidade) que envolva três grandezas que variam de forma proporcional (direta ou inversamente).
Elabore um problema de regra de três composta usando essas grandezas, de modo que um colega consiga resolvê-lo.
Seu enunciado deve conter:
- a situação descrita;
- os valores conhecidos;
- o que deve ser descoberto.
Depois, troque o problema com um colega da turma e resolvam as situações elaboradas.
| Autoria | Cristiane Soares de Souza |
| Formação | Licenciatura em Matemática |
| Componente curricular | Matemática |
| Objeto(s) de conhecimento | Grandezas proporcionais, regra de três composta. |
| Habilidade(s) | (EF09MA08-A) Reconhecer o uso das regras de três simples e compostas em situações problema que envolvam relações de proporcionalidade direta ou inversa entre duas ou mais grandezas. (EF09MA08-B) Ler, interpretar, resolver e elaborar problemas que envolvam relações de proporcionalidade direta e inversa entre duas ou mais grandezas, inclusive escalas, divisão em partes proporcionais e taxa de variação, em contextos socioculturais, ambientais e de outras áreas. |
| Descritor(es) | D29 – Resolver problema que envolva variação proporcional, direta ou inversa, entre grandezas. |
| Referências | SILVEIRA, Ênio. Matemática: compreensão e prática. 5ª edição, São Paulo, Moderna, 2018. III SIPEMAT (Simpósio Internacional de Pesquisa em Educação Matemática). LAVOR, Otávio Paulino. et al. Grandezas proporcionais e objetos de aprendizagem: uma experiência com alunos do ensino fundamental. URL https://proativa.virtual.ufc.br/sipemat2012/papers/130/submission/director/130.pdf, consultado em 20/08/2025. |

