Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 7º Ano do Ensino Fundamental – Anos Finais.
Números Racionais
Em algumas situações, é preciso ter precisão na medida ou na contagem. Veja só um exemplo: dividir R$100,00 igualmente entre 3 pessoas. Esta não é uma divisão exata.
Se for considerar apenas a parte inteira, cada pessoa receberia R$ 33,00 e sobraria R$1,00. Para ser justo e repartir com mais precisão, dividindo a sobra R$1,00 entre as 3 pessoas, chegaremos a um número decimal e infinito.
Foi para agrupar esse tipo de número que surgiu o conjunto dos números racionais. Neste conjunto estão incluídos todos os números que podem ser escritos na forma de fração, ou seja, todo número que é resultado divisão entre dois números inteiros (denominador / divisor diferente de zero).
Pertencem ao conjunto dos números os que inclui:
- as frações como 3/4, 5/2;
- os números decimais finitos como 0,5 ou 2,75;
- as dízimas periódicas como 0,333…;
- e também os números inteiros, como -3, 0, 7.
As porcentagens são frações centesimais (denominador 100). Logo, é uma forma de escrever um número racional.
Formas de representar um número racional
Um mesmo número racional pode ser escrito de formas diferentes sem alterar o seu valor.
Veja esse exemplo, a “metade” de uma goiaba.

Essas representações nos ajudam a entender melhor como os números são usados em diferentes contextos, como: frações aparecem em receitas de bolo, decimais nas etiquetas de preço e porcentagens em descontos e aumentos.
Transformando os números racionais
- De fração para decimal: dividir o numerador pelo denominador
1/4 = 0,25
- De decimal finito para fração: escrever o número sem vírgula no numerador e, no denominador, 1 seguido de tantos zeros quantos forem os algarismos nas casas decimais.

Comparando e ordenando números racionais
Reveja o conceito de número racional assistindo a videoaula da professora Cristiane Souza, “Comparações de números racionais”, do canal Estúdio Conexão Escola, no YouTube.
Agora, resolva as atividades a seguir.
QUESTÃO 1
Na fração 4/3, dividindo numerador pelo denominador temos
(A) um número inteiro.
(B) um número decimal finito.
(C) um número decimal infinito.
(D) uma raiz quadrada.
QUESTÃO 2
Os números na lista abaixo não estão em ordem.
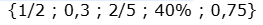
Reescreva a sequência em ordem crescente.
QUESTÃO 3
Leia com atenção as alternativas abaixo. Compare os valores apresentados completando as lacunas com os símbolos > (maior que), < (menor que) ou = (igual a).
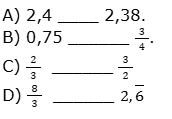
QUESTÃO 4
Leia com atenção as dicas a seguir. Elas descrevem um número racional que está escondido.
- É uma dízima periódica com um único algarismo se repetindo.
- É maior que 0,3 e menor que 0,4.
- Sua forma fracionária é 1/3.
Agora responda, que número racional é esse?
QUESTÃO 5
Para cada número abaixo, classifique-os em “número inteiro”, “número decimal finito”, “dízima periódica”.

QUESTÃO 6
Complete as lacunas da tabela com as representações indicadas.

QUESTÃO 7
O decimal 0,125 corresponde à fração
(A) 1/8.
(B) 3/5.
(C) 5/4.
(D) 15/10.
| Autoria | Cristiane Soares de Souza |
| Formação | Matemática |
| Componente Curricular | Matemática |
| Habilidades | (EF07MA05-A) Reconhecer que os números racionais positivos podem ser expressos nas formas: fracionária, percentual, decimal exata e dízima períodica. (EF07MA08) Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador. |
| Descritor | D17 – Identificar a localização de números racionais na reta numérica. D21 – Reconhecer as diferentes representações de um número racional. |
| Objetos de conhecimento | Números racionais: conceito; formas de representação (fracionária e decimal); conversão de fração para número decimal, decimal para fração, porcentagem para fração e decimal, comparação e ordenação de números racionais. |
| Referências | NEPEM: Núcleo de Estudos e Pesquisas em Educação Matemática, UFS. Números Racionais no Ensino Fundamental: subconstructos, o papel da linguagem e dos materiais manipulativos. 2004. SBEM VII Encontro de Educação Matemática. Disponível em https://www.sbembrasil.org.br/files/viii/pdf/02/CC07976229850.pdf, consultado em 06/05/25. SOUZA, Bruna Queiroz de. FROIS, Patrícia Duarte Petrucelli. Números Racionais: conceitos e representações. FE USP. Disponível em http://www.labeduc.fe.usp.br/wp-content/uploads/Unidade-did%C3%A1tica-N%C3%BAmeros-Racionais-Conceitos-e-representa%C3%A7%C3%B5es-1.pdf, consultado em 06/05/25. |

