Esta proposta de atividade de Matemática, elaborada com base no DC/GO – Ampliado, é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Os Números Reais
O conjunto dos números reais é formado por todos os números que usamos no cotidiano:

Esses números podem ser agrupados em dois grandes grupos: os números racionais e os irracionais.
Os números racionais:
Número racional é todo número que pode ser escrito na forma de fração em que numerador e denominador são inteiros. Racional vem de razão, ou seja, resultado de uma divisão entre dois números inteiros. Isso inclui:
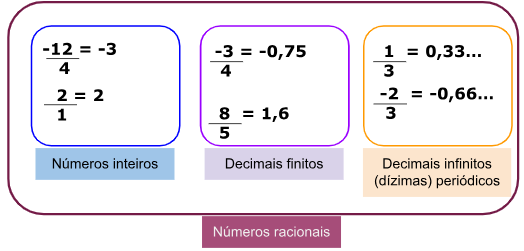
Os números irracionais:
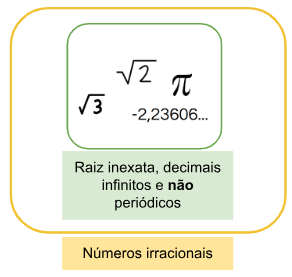
O conjunto dos números irracionais é formado pelos números que não podem ser escritos na forma de fração. Ou seja, não são resultados de uma divisão simples entre dois números inteiros. Neste grupo estão as raízes inexatas e as chamadas dízimas não periódicas (números decimais infinitos sem padrão de repetição).
Localização na reta numérica
Os números têm lugar na reta numérica. Os números inteiros têm lugar bem determinado. Já as frações que resultam em números decimais, terão lugar entre números inteiros. Vejamos como marcar essa sequência de números:
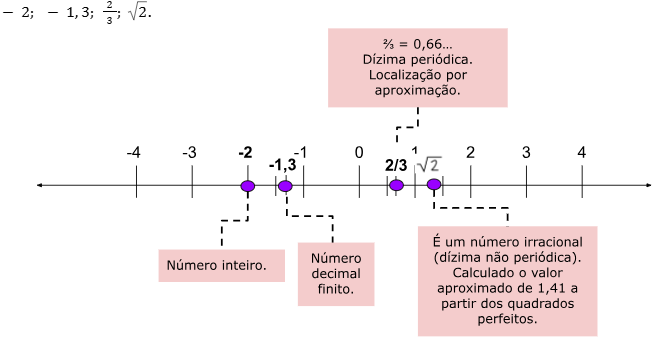
Bom, se quiser rever o conceito de números racionais e as suas representações, assista à videoaula da professora Cristiane Souza, “Números racionais”, do canal Estúdio Conexão Escola, no YouTube, que segue aqui abaixo.
Agora, que tal exercitar os conhecimentos adquiridos resolvendo a estes exercícios? Mãos à obra!
QUESTÃO 1
A alternativa que contém um número irracional é
(A) -1,33…
(B) 2.
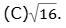
(D) 3,14159…
QUESTÃO 2
Alguns números decimais e frações estão entre dois números inteiros consecutivos. Observe os exemplos e complete:
A) O número –1,6 está localizado entre os inteiros _____ e _____.
B) A fração 7/3 equivale a um número decimal. Ela está localizada entre os inteiros _____ e _____.
C) O número √5 é irracional. Ele está localizado entre os inteiros _____ e _____.
QUESTÃO 3

QUESTÃO 4
Observe a reta numérica a seguir. Nela estão marcados alguns pontos.

Os pontos A e B, nesta ordem, são iguais a
(A) -3 e ⅔.
(B) -⅗ e ⅔ .
(C) -3,5 e 2,3.
(D) -⅗ e 2.
QUESTÃO 5
Escreva os números a seguir na forma de fração irredutível:
A) 2,75 =
B) -0,4 =
C) 1,25 =
QUESTÃO 6
Glaucia pratica corrida regularmente. A sua meta é correr 42 km por semana. Ela já correu ⅔ dessa distância.
A) Qual distância, em km, Glaucia já correu?
B) Quantos quilômetros faltam para Glaucia atingir a meta da semana?
QUESTÃO 7
Em uma receita, as quantidades de ingredientes líquidos são:
¾ de xícara de chá de leite
½ xícara de chá de óleo.
A) Calcule a quantidade total de ingredientes líquidos em xícaras.
B) Uma xícara de chá tem 250ml aproximadamente. Calcule o total de ingredientes líquidos em ml.
SAIBA MAIS
Você já ouviu falar no filósofo Hipaso de Metaponto? Pois bem, este filósofo grego faz parte da história dos números irracionais. A ele é atribuída a descoberta desses números por ser o primeiro comprovar a existência dos irracionais. No programa Deu Mat!, do Conexão Escola, há um programa dedicado aos números irracionais, “Números Irracionais e Hipaso de Metaponto”. Fica a dica para conhecer essa história do filósofo e o número irracional.
| Autoria: | Cristiane S de Souza |
| Formação: | Matemática – Licenciatura |
| Componente curricular: | Matemática |
| Habilidade(s): | (EF09MA02-A) Reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica (dízima periódica) e que pode ser escrita em forma de fração irredutível a/b, com b diferente de zero. (EF09MA02-B) Aplicar a localização de números racionais para estimar a localização de alguns números irracionais na reta numérica. (EF09MA02-C) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica em situações diversas. (EF06MA08-C) Relacionar os números racionais positivos expressos nas formas, fracionária e decimal, a pontos na reta numérica. |
| Descritor(es): | D17 – Identificar a localização de números racionais na reta numérica. |
| Objeto(s) de conhecimento: | Números racionais: conceito, formas de representação (fracionária e decimal), conversão de fração para número decimal e vice-versa, operações com racionais. |
| Referência(s): | NEPEM: Núcleo de Estudos e Pesquisas em Educação Matemática, UFS. Números Racionais no Ensino Fundamental: subconstructos, o papel da linguagem e dos materiais manipulativos. 2004. SBEM VII Encontro de Educação Matemática. Disponível em https://www.sbembrasil.org.br/files/viii/pdf/02/CC07976229850.pdf, consultado em 06/05/25. SOUZA, Bruna Queiroz de. FROIS, Patrícia Duarte Petrucelli. Números Racionais: conceitos e representações. FE USP. Disponível em http://www.labeduc.fe.usp.br/wp-content/uploads/Unidade-did%C3%A1tica-N%C3%BAmeros-Racionais-Conceitos-e-representa%C3%A7%C3%B5es-1.pdf, consultado em 06/05/25. |

