Esta proposta de atividade de matemática é destinada aos estudantes do 4º ano do Ensino Fundamental.

Prismas e Pirâmides
Você já reparou como muitos elementos do nosso dia a dia têm formas parecidas com caixas, telhados ou pirâmides do Egito? Pois é! Essas formas têm nomes especiais: prismas e pirâmides. E hoje vamos aprender a desenhar, abrir e explorar essas figuras de um jeito bem divertido!
O prisma é uma figura que tem duas bases (em cima e embaixo) com a mesma forma. Por exemplo, se a base for um triângulo, chamamos de prisma triangular. Se for um quadrado, é prisma quadrado! As outras partes do prisma são as faces laterais, e elas sempre são retângulos. Já os cantinhos onde as linhas se encontram chamamos de vértices, e as linhas que ligam os vértices são as arestas.
A pirâmide é diferente. Ela tem apenas uma base, e todas as outras faces são triângulos, que se encontram lá no alto, formando uma pontinha.
Agora, imagine que você tem uma caixinha e vai desmontá-la para ver como ela seria se estivesse aberta no papel. Isso se chama planificação. Ao abrir um prisma ou uma pirâmide, conseguimos ver todas as suas partes separadas — isso ajuda a entender melhor as formas, os lados e os ângulos.
E sabe o que é mais legal? Você pode desenhar essas figuras usando régua, compasso, esquadros ou até aplicativos de computador! Que tal treinar um pouco agora?
RESPONDA ÀS QUESTÕES:
QUESTÃO 1
Um prisma é uma figura que tem
A) uma base e lados triangulares.
B) várias pontas em cima.
C) duas bases iguais e lados retangulares.
D) apenas uma face redonda.
QUESTÃO 2
Uma pirâmide com base quadrada tem
A) quatro triângulos e um quadrado.
B) cinco retângulos.
C) quatro círculos e um triângulo.
D) duas bases iguais.
QUESTÃO 3
Desenhe uma pirâmide com base quadrada. Depois, ao lado, desenhe como ela ficaria aberta, ou seja, em forma de planificação. Lembre-se de mostrar o quadrado da base e os quatro triângulos das laterais!
QUESTÃO 4
Desafio de raciocínio!
Observe a descrição da figura:
“Tem 6 vértices, 9 arestas e 5 faces.”
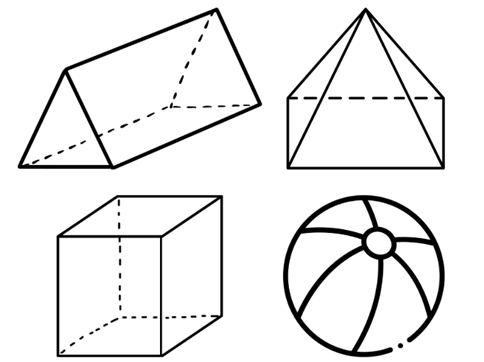
Qual figura é essa?
a) Prisma triangular.
b) Pirâmide com base quadrada.
c) Cubo.
d) Bola.
QUESTÃO 5
Descubra a quantidade de partes de um prisma!
Um prisma pentagonal tem:
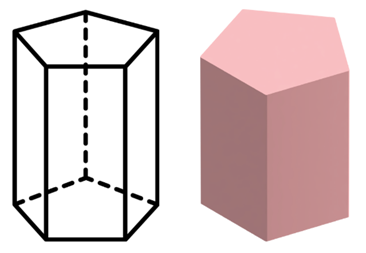
___ vértices
___ arestas
___ faces
QUESTÃO 6
Para que serve aprender a desenhar e abrir figuras como prismas e pirâmides? Escreva com suas palavras o que você aprendeu e onde você vê essas formas na vida real (ex: caixa de leite…).
QUESTÃO 7
Observe as planificações abaixo e descubra qual é o nome da pirâmide que cada uma forma quando montada.
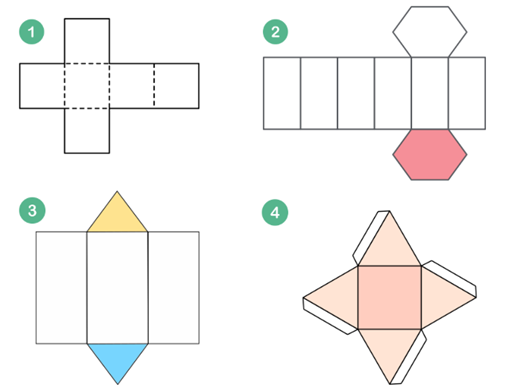
ASSISTA A VIDEOAULA SOBRE ESSE CONTEÚDO:
| Autoria: | Prof.ª Esp. Danielle Assis Borges Fantini |
| Formação: | Graduanda em Nutrição. Graduada em Jornalismo e Pedagogia. Pós-graduada em: – MBA em Gestão das Tecnologias da Informação e da Comunicação – Educação; – Docência Universitária; – Psicopedagogia Institucional e Clínica; – Neuropedagogia Aplicada à Educação. |
| Componente Curricular: | Matemática |
| Conteúdo(s)/objeto(s) de conhecimento: | Figuras geométricas espaciais (prismas e pirâmides): reconhecimento, representações, planificações e características |
| Habilidade(s)/objetivo(s) de aprendizagem e desenvolvimento: | DOCUMENTO CURRICULAR PARA GOIÁS – AMPLIADO: (EF04MA17-A) Representar prismas e pirâmides por desenho, com recursos específicos, tais como régua, compasso, esquadros ou tecnologias digitais. (EF04MA17-B) Representar as planificações de prismas e pirâmides, para reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos. |
| Descritor(es): | D2: Identificar propriedades comuns e diferenças entre poliedros e corpos redondos, relacionando figuras tridimensionais com suas planificações. |
| Referências: | BRASIL. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira – INEP. Matriz de Referência de Matemática. Brasília: INEP, [s.d.]. Disponível em: https://download.inep.gov.br/educacao_basica/prova_brasil_saeb/menu_do_professor/o_que_cai_nas_provas/Matriz_de_Referencia_de_Matematica.pdf. Acesso em: 24 abr. 2025. CANVA. Ferramenta de design gráfico online. Disponível em: https://www.canva.com/. Acesso em: 24, abr. 2025. GIOVANNI JÚNIOR, José Ruy. A conquista: matemática: 4º ano: ensino fundamental. 1. ed. São Paulo: FTD, 2021. GOIÁS. Secretaria de Estado da Educação. Documento Curricular para Goiás: ampliado – Etapa Ensino Fundamental: anos finais. Goiânia: Seduc, 2019. PASSOS, Célia; SILVA, Zeneide. Eu gosto mais: matemática: 4º ano: ensino fundamental. 5. ed. São Paulo: IBEP, 2022. |
