Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Introdução
Este texto explora as relações no triângulo retângulo, uma figura essencial na matemática. A partir do Teorema de Pitágoras e das propriedades de seus lados e ângulos, veremos como essas relações são fundamentais para resolver problemas e compreender melhor a geometria.
Imagem do autor produzida no Geogebra
O triângulo retângulo (só para lembrar!)
Um triângulo retângulo é um triângulo que possui um ângulo de 90 graus, ou seja, um ângulo reto. Ele é composto por três lados: o maior deles é chamado de hipotenusa, que está oposto ao ângulo reto, e os outros dois lados menores, chamados de catetos.
Imagem do autor produzida no Geogebra
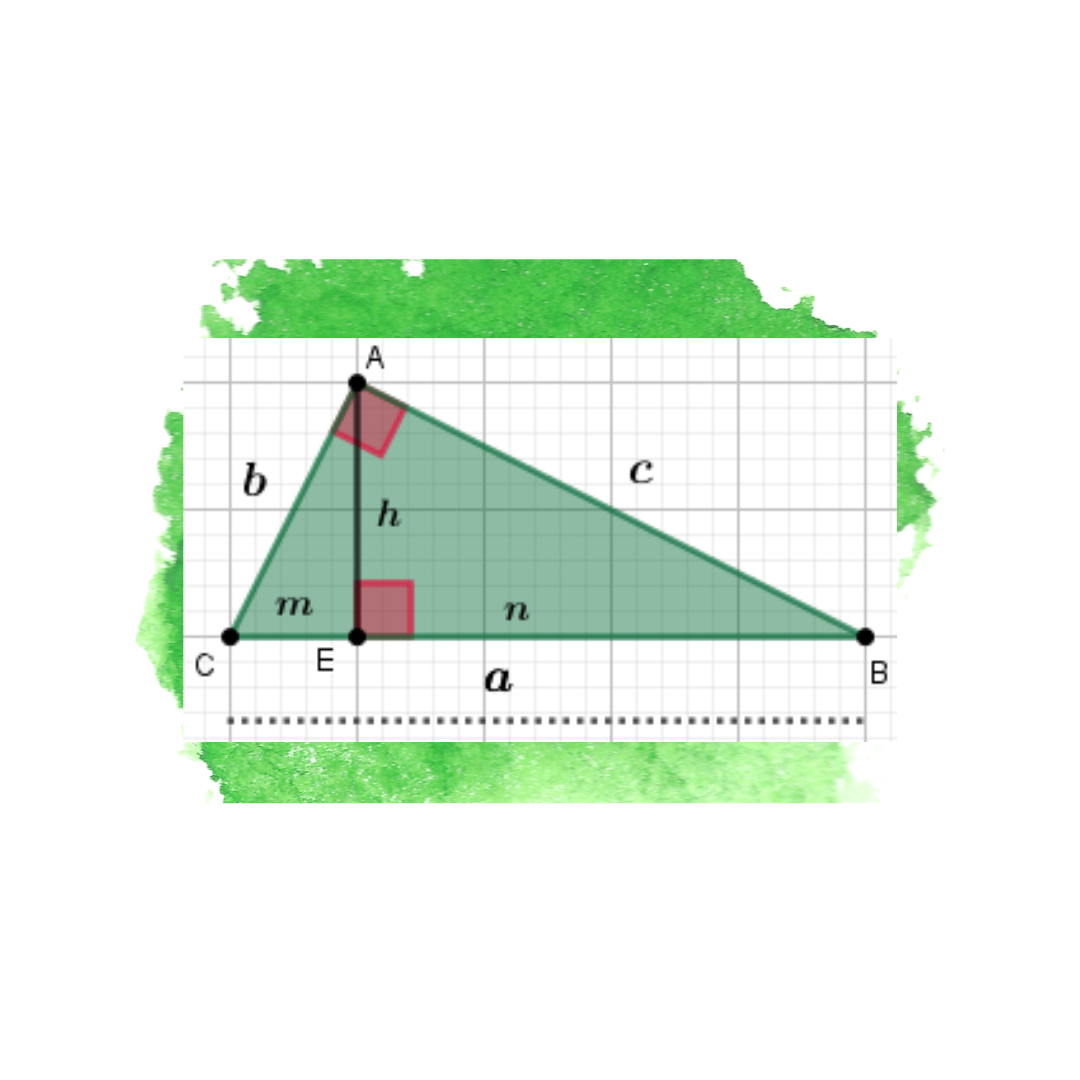
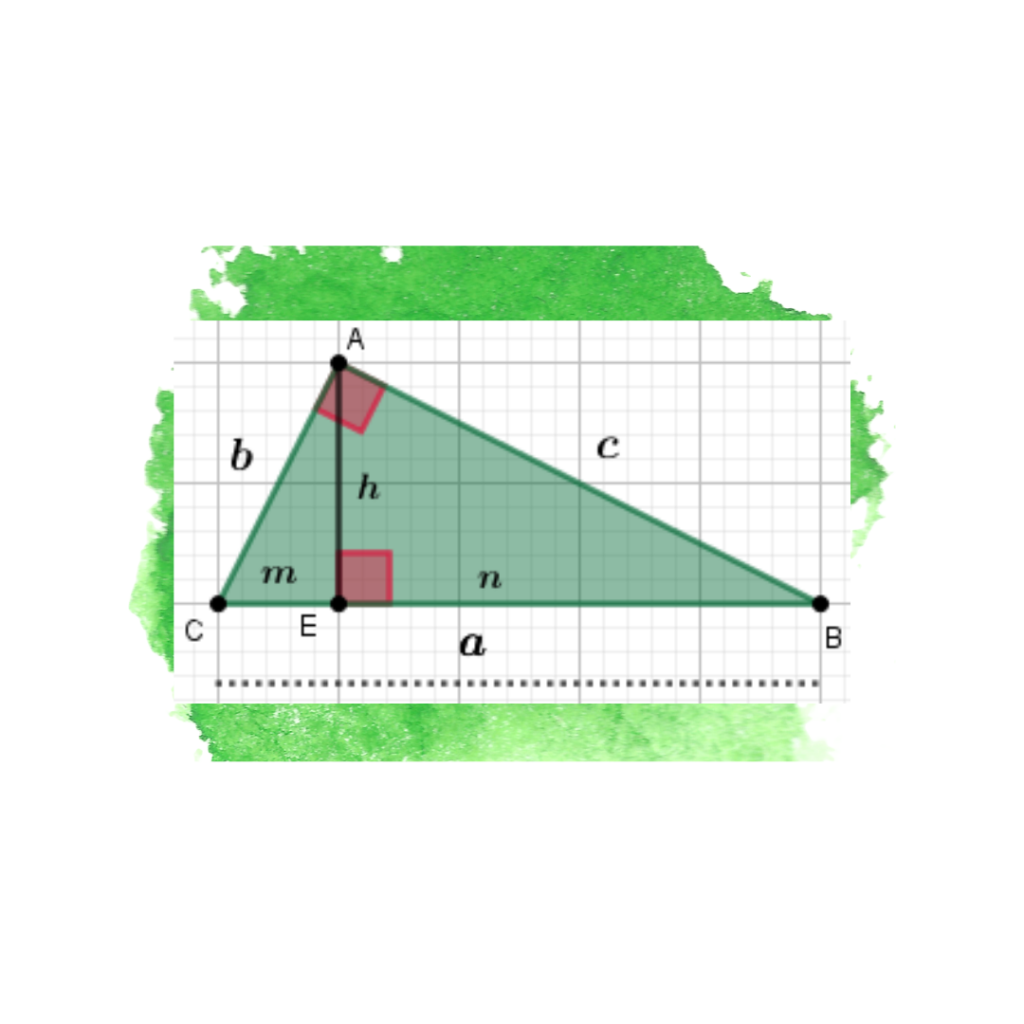
A altura e as projeções dos catetos
Ao traçar a altura (h) do triângulo retângulo a partir do vértice do ângulo reto até a hipotenusa, o triângulo se divide em dois triângulos menores, ambos semelhantes ao triângulo original. Essa altura cria duas projeções (m e n) dos catetos sobre a hipotenusa, chamadas de projeções dos catetos.
Imagem do autor produzida no Geogebra
As relações métricas
As relações métricas no triângulo retângulo mostram como seus lados e ângulos estão conectados. Nesta parte, vamos explorar o Teorema de Pitágoras, as projeções dos catetos na hipotenusa e a altura que parte do ângulo reto até a hipotenusa.
1ª Relação: O Teorema de Pitágoras
Em um triângulo retângulo, o quadrado da medida da hipotenusa (a) é igual à soma dos quadrados das medidas dos catetos (b e c).
Imagem do autor produzida no Geogebra
Existem diversas maneiras de se demonstrar este Teorema, neste texto não iremos abordar essa demonstração.
2ª Relação: Altura relativa à hipotenusa e as projeções dos catetos.
Como foi dito anteriormente, ao traçar a altura relativa a hipotenusa, o triângulo retângulo se divide em dois triângulos menores, ambos semelhantes ao triângulo original. Aplicando a semelhança de triângulos, podemos afirmar que:
Em um triângulo retângulo, o quadrado da altura (h) relativa à hipotenusa é igual ao produto das projeções (m e n) dos catetos sobre a hipotenusa.
Imagem do autor produzida no Geogebra
3ª relação: As projeções dos catetos e a hipotenusa.
Ainda por semelhança de triângulos, podemos afirmar que:
O quadrado de cada cateto (b e c) de um triângulo retângulo é igual ao produto da hipotenusa (a) pela projeção do cateto (m ou n) sobre a hipotenusa.
Imagem do autor produzida no Geogebra
4ª relação: O produto dos catetos e o produto entre a hipotenusa e a altura.
Ainda por semelhança de triângulos, podemos afirmar que:
O produto dos catetos (b e c) de um triângulo retângulo é igual ao produto da hipotenusa (a) pela altura (h) relativa à hipotenusa.
Imagem do autor produzida no Geogebra
Um problema para finalizar
Em um triângulo retângulo, a hipotenusa mede 17 cm e um dos catetos tem 8 cm. Com essas informações, determine:
A) O valor do outro cateto.
B) As projeções m e n dos catetos sobre a hipotenusa.
C) A altura relativa à hipotenusa.
Resolução:
Colocando estes dados em uma figura e aplicando as relações apresentadas acima, temos:
Imagem do autor produzida no Geogebra
A) Para determinar a medida do outro cateto, basta aplicar o Teorema de Pitágoras:
B) Para determinar a medida das projeções, utilizaremos a 3ª relação:
C) Para determinar a medida da altura, utilizaremos a 2ª relação:
Ficamos por aqui, até o próximo.
QUESTÃO 1
Um bombeiro precisa resgatar um gato preso em uma árvore. Ele posiciona uma escada a 4 metros de distância da base da árvore, e a escada deve alcançar um ponto que está a 5 metros de altura. Qual deve ser o comprimento mínimo da escada para que o bombeiro consiga alcançar o gato?
Ajuda: Faça um desenho e projete nele um triângulo retângulo para aplicar o teorema de Pitágoras.
QUESTÃO 2
Em uma área de construção, um engenheiro quer calcular a altura de uma parede inclinada em relação ao solo para determinar o ponto exato onde instalar um suporte. Ele sabe que a base da parede mede 10 metros (hipotenusa) e que uma de suas partes, projetada no solo por um dos suportes de um andaime, mede 4 metros. Qual é a altura perpendicular da parede em relação ao solo?
Ajuda: Faça um desenho e projete nele um triângulo retângulo para aplicar a relação entre a altura e as projeções.
QUESTÃO 3
Em um triângulo retângulo, se um cateto mede 6 cm e sua projeção na hipotenusa mede 3 cm, podemos afirmar que o quadrado do cateto é igual
(A) ao triplo da hipotenusa.
(B) ao dobro da altura.
(C) ao produto da hipotenusa pela projeção.
(D) à soma da altura e da hipotenusa.
QUESTÃO 4
Em um triângulo retângulo, o produto da hipotenusa pela altura em relação a ela é igual
(A) à soma dos catetos.
(B) ao quadrado de um dos catetos.
(C) ao produto dos catetos.
(D) à soma dos ângulos internos.
| Autoria: | Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA13) Demonstrar relações métricas do triângulo retângulo, entre elas o Teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |