ESTA PROPOSTA DE ATIVIDADE DE MATEMÁTICA, INTEGRADA COM CIÊNCIAS, É DESTINADA AOS ESTUDANTES DO 2º PERÍODO (3ª SÉRIE) DA EDUCAÇÃO DE JOVENS E ADULTOS – EJA.
Simetria de Reflexão
A simetria é uma característica que faz com que algo possa ser dividido em partes idênticas. Isto quer dizer que as partes têm o mesmo tamanho e formato. Vejamos alguns exemplos simples de simetria.
O triângulo isósceles é uma figura geométrica simétrica. Traçando uma linha passando pelo meio do triângulo, este será dividido em duas metades iguais. Essa linha de divisão é chamada de eixo de simetria.
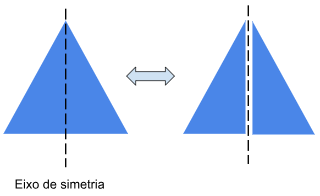
Imagem 1: Simetria no triângulo isósceles – produzida no Google Desenhos.
Se dobrar o triângulo ao meio, as duas metades vão se sobrepor, coincidindo perfeitamente. Isto porque, uma parte é o reflexo da outra. Este é um exemplo de simetria de reflexão.
A simetria também está presente na natureza. Veja só essa borboleta.

Imagem 2: Simetria na borboleta – produzida no canva.com
As duas metades da borboleta são idênticas, uma é o reflexo da outra. Sobrepondo, as asas coincidem perfeitamente. Logo, a borboleta tem simetria por reflexão.
Na simetria de reflexão, o eixo de simetria funciona como um “espelho” refletindo as partes divididas.
Podemos encontrar a simetria de reflexão em vários lugares, na geometria, na natureza (plantas, animais, inclusive no corpo humano), nas artes, na engenharia, no design e etc. A simetria é importante porque traz equilíbrio e harmonia visual, sendo uma maneira de deixar as formas mais organizadas e agradáveis aos nossos olhos.
Bom estudo!
QUESTÃO 1
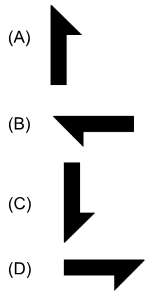
A figura apresentada abaixo foi dividida ao longo de seu eixo de simetria na horizontal, resultando em duas partes idênticas. Essa simetria é chamada de simetria por reflexão.

Com base nessa informação, a parte que completa a figura, de modo que as duas metades sejam reflexos perfeitos uma da outra, é
QUESTÃO 2
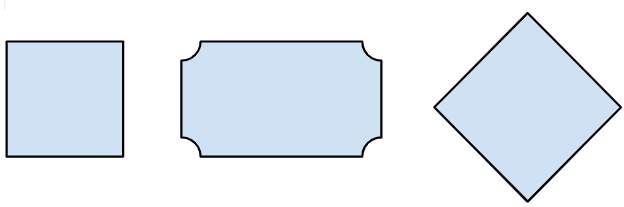
Eixo de simetria é o nome dado à reta que divide uma forma em duas partes iguais, tanto no formato quanto nas medidas.
Sendo assim, observe as imagens abaixo e, para cada uma delas, desenhe os eixos de simetria que conseguir identificar.
Sugestão: use uma régua.
QUESTÃO 3
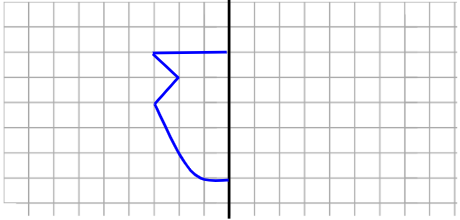
A figura na malha quadriculada apresenta simetria por reflexão. Apenas metade da figura foi desenhada. Agora, complete a imagem desenhando o seu reflexo, de modo que as duas partes sejam simétricas.
QUESTÃO 4
O grafite é uma forma de arte urbana em que artistas utilizam os muros e espaços públicos para expressar suas ideias e criatividade através de desenhos e pinturas. Muitas vezes, os grafites possuem formas geométricas e simétricas.
Agora é a sua vez de criar! Desenhe metade do seu próprio grafite, utilizando sua imaginação. Em seguida, aplique o conceito de simetria por reflexão para espelhar o outro lado, de forma que as duas partes fiquem iguais, como se uma fosse o reflexo da outra.
QUESTÃO 5
Qual tipo de simetria que se pode observar na borboleta?
(A) Simetria de rotação.
(B) Simetria de translação.
(C) Simetria de reflexão.
(D) Simetria de compensação.
| AUTORIA | CRISTIANE SOARES DE SOUZA, LICENCIATURA DE MATEMÁTICA |
| COMPONENTE CURRICULAR | MATEMÁTICA E ARTE |
| OBJETIVOS DE APRENDIZAGEM E DESENVOLVIMENTO | (EJAMA0226) Reconhecer simetria de reflexão em objetos familiares e construir pares de figuras geométricas planas. (EJAAD0212) Vivenciar distintas manifestações de expressão, percepção e consciência do corpo a partir do estudo da cultura urbana e suas manifestações artísticas. |
| REFERÊNCIAS | GARCIA, Cássia de Souza, et al. É bom renovar, edição renovada, Educação de Jovens e Adultos, volume 2, 2014, FTD – São Paulo. LARA, Arthur Hunold. Arte Urbana em Movimento. Escola de Comunicações e Artes da USP – Universidade de São Paulo, 1996. OLIVEIRA, Raul Rodrigues de. “Simetria”; Brasil Escola. Disponível em http://brasilescola.uol.com.br/matematica/simetria.htm. Acesso em 02/10/24. RIZZO, Maria Luiza Alves. Simetria: o que é, tipos e exemplos. Prepara ENEM. Disponível em https://www.preparaenem.com/matematica/simetria.htm. Acesso em 02/10/24. SALLES, Eliciane Bruning de. et al. Arte e Matemática: o ensino de simetria é magia. IV Jornada Nacional de Educação Matemática e XVII Jornada Regional de Educação Matemática – Universidade de Passo Fundo. Disponível em http://anaisjem.upf.br/download/sp-43-salles.pdf, acesso em 03/10/24. |
