Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 5º período da Educação de Jovens e Adultos – EJA
Introdução
Neste texto, vamos aprender sobre o volume e a capacidade de objetos que têm a forma de cilindro reto. Definiremos volume e capacidade e como calcular, além de entender a relação entre volume e capacidade com exemplos práticos. No final, você encontrará dois problemas do dia a dia resolvidos.
Imagem:canva.com/cilindro
O Que é Volume?
O volume é a medida do espaço ocupado por um objeto.
No caso dos cilindros, o volume depende do tamanho da base circular e da altura do cilindro. A base é o círculo na parte de baixo, e a altura é a distância entre a base e o topo do cilindro.
As unidades de volume mais utilizadas são:
- o m3 ( metro cúbico),
- o dm3 (decímetro cúbico) e
- o cm3 (centímetro cúbico).
Como Calcular o Volume de um Cilindro?
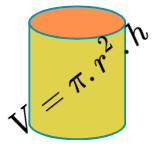
Para calcular o volume de um cilindro reto, usamos a seguinte fórmula:
Onde, nesta fórmula:
O que é Capacidade?
A Capacidade é a quantidade de líquido que um objeto pode armazenar.
As unidades de capacidade mais utilizadas são:
- o L (litro) e
- o mL (mililitro).
Relação entre as unidades de medida de volume e capacidade
- 1 m3 = 1000 L
- 1 cm3 = 1 mL
- 1 dm3 = 1 L
Problemas do Cotidiano
Problema 1: Caixa d’água cilíndrica
Uma caixa d’água em forma de cilindro tem um raio de 50 cm e uma altura de 100 cm. Qual é o volume de água que essa caixa pode armazenar?
Resolução:
Usamos a fórmula do volume de um cilindro:
V = 3,14 . 502 . 100 = 3,14 . 2500 . 100 = 7850 . 100 = 785000 cm3.
Resposta:
Como 1 litro é igual a 1000 cm³, o volume da caixa d’água é de 785 litros (785000:1000).
Problema 2: Copo de plástico
Um copo descartável tem 4 cm de raio na base e 10 cm de altura. Qual é a capacidade máxima de líquido que esse copo pode conter?
Resolução: Usamos a fórmula do volume:
V = 3,14 . 43 . 10 = 3,14 . 16 . 10 = 50,24 . 10 = 502,4 cm3.
Resposta:
Como 1 cm3 é igual a 1 mL, o copo pode conter 502,4 mL, ou seja, aproximadamente 0,502 litros, o que é um pouco a mais do que meio litro de líquido.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
Uma lata de óleo tem a forma de um cilindro.
A) Se a lata tem 10 cm de altura e o raio da base mede 5 cm, qual é o volume de óleo que ela pode conter?
B) Se cada mililitro de óleo corresponde a 1 cm³ de volume, quantos mililitros de óleo cabem na lata?
QUESTÃO 02
Um tanque de combustível de um carro tem a forma de um cilindro.
A) Se o tanque tem 50 cm de comprimento e o raio da base mede 20 cm, qual é a capacidade do tanque em litros? (Considere que 1 dm³ equivale a 1 litro.)
B) Se o tanque está com metade da sua capacidade, quantos litros de combustível faltam para enchê-lo?
QUESTÃO 03
Um tanque de água em formato cilíndrico tem 2 metros de altura e raio da base de 1,5 metros. A capacidade desse tanque, em litros, é
(A) 14130 litros.
(B) 7065 litros.
(C) 3532,5 litros.
(D) 2826 litros.
QUESTÃO 04
Uma vela em formato de cilindro tem 12 cm de altura e raio da base de 2 cm. Se a vela queima completamente a uma taxa de 2 cm³ por hora, o tempo aproximado que a vela levará para se consumir completamente é de
(A) 150 horas.
(B) 75 horas.
(C) 30 horas.
(D) 15 horas.
SAIBA MAIS
Assista ao vídeo para aprender um pouco mais sobre Volume e Capacidade
| Autoria | Professor Hélio Roberto da Rocha, Mestre em Matemática. |
| Componente Curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0527) Interpretar, resolver e elaborar situações-problema que envolvam o cálculo do volume de recipientes cujo formato é de bloco retangular ou de cilindro reto. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9º ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9° ano – Ensino Fundamental; Matemática; Goiânia, 2024. |

