Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 5º período da Educação de Jovens e Adultos – EJA

Introdução
Neste texto, vamos explorar o cálculo de áreas dos quadriláteros e triângulos. Abordaremos inicialmente o conceito de área e suas unidades de medida, e, em seguida, passaremos às fórmulas e exemplos práticos para o cálculo da área desses polígonos.
Imagem produzida no canva.com/quadriláteros
Conceito de Área e Unidades de Medida
A área é uma medida da extensão de uma superfície. Quando falamos da área de uma figura plana, estamos nos referindo à quantidade de espaço contido dentro de seus limites. Essa quantidade é expressa em unidades quadradas, como metros quadrados (m²), centímetros quadrados (cm²) ou quilômetros quadrados (km²), dependendo do contexto e da dimensão da figura que estamos analisando.
Área dos Quadriláteros
- Retângulo: sua área é dada pela multiplicação da base (comprimento) pela altura (largura).
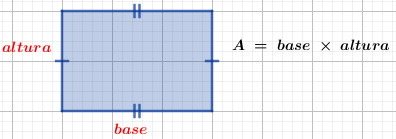
Imagem do Autor produzida no Geogebra
- Quadrado: é um caso especial do retângulo onde todos os lados têm o mesmo comprimento. A fórmula da área de um quadrado é a multiplicação de um lado por ele mesmo.
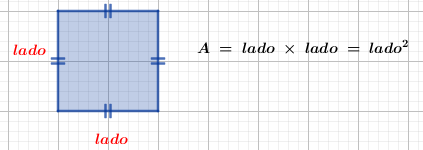
Imagem do Autor produzida no Geogebra
- Paralelogramo: semelhante ao retângulo, mas com lados opostos inclinados. A área é calculada pela multiplicação da base pela altura perpendicular à base.
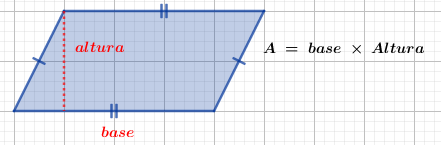
Imagem do Autor produzida no Geogebra
- Trapézio, sua área é calculada pela média aritmética das bases multiplicada pela altura.
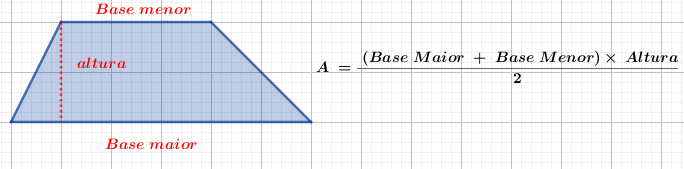
Imagem do Autor produzida no Geogebra
Área dos Triângulos
- Triângulos sua a área é dada pela metade do produto entre as medidas da sua base e da sua altura.
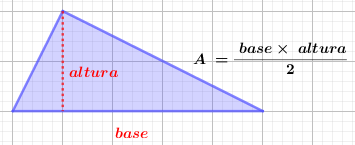
Imagem do Autor produzida no Geogebra
OBS
- A base pode ser qualquer um dos lados do triângulo, e a altura é a distância perpendicular entre essa base e o vértice oposto.
- Independentemente do tipo de triângulo (equilátero, isósceles ou escaleno), a fórmula para o cálculo da área permanece a mesma.
Um problema para finalizar
João deseja pintar a parede retangular de seu quarto. A parede tem 4 metros de comprimento e 2,5 metros de altura. Para calcular a quantidade de tinta necessária, ele precisa descobrir a área total da parede. Sabendo que litro de tinta cobre 5 metros quadrados, quantos litros de tinta João precisará comprar para pintar a parede?
Resolução:
Cálculo da área da parede (retângulo)
Área=4 × 2,5 m2
Cálculo da quantidade de tinta
Foi informado que cada litro de tinta cobre 10 metros quadrados, logo João irá precisar de 10 : 5 = 2 litros de tinta.
Resposta: João irá precisar de 2 litros de tinta para pintar toda a parede.
Conclusão
Entender como calcular a área de quadriláteros e triângulos é essencial para resolver problemas práticos do dia a dia, como calcular o espaço necessário para cobrir uma superfície ou planejar a utilização de áreas em projetos.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
A sala de aula de João tem formato quadrado e cada lado mede 6 metros. A área total da sala é de
(A) 12 metros quadrados.
(B) 24 metros quadrados.
(C) 36 metros quadrados.
(D) 48 metros quadrados.
QUESTÃO 02
Um retângulo tem área de 32 cm² e um dos lados mede 8 cm. O outro lado desse retângulo mede
(A) 24 cm.
(B) 16 cm.
(C) 4 cm.
(D) 8 cm.
QUESTÃO 03
Um pedreiro precisa revestir o chão de uma cozinha que tem formato retangular. A cozinha mede 4 metros de comprimento e 3 metros de largura. Cada cerâmica quadrada que ele vai usar tem lado de 20 centímetros.
A) Qual é a área total da cozinha em metros quadrados?
B) Quantas cerâmicas serão necessárias para revestir toda a cozinha?
QUESTÃO 04
Um construtor precisa pintar uma parede da sala que tem formato retangular. A parede mede 3 metros de altura e 5 metros de largura. Cada lata de tinta cobre 8 metros quadrados.
A) Qual é a área da parede a ser pintada?
B) Quantas latas de tinta serão necessárias para pintar toda a parede?
SAIBA MAIS
Assista ao vídeo para aprender um pouco mais sobre Cálculos de Áreas
| Autoria | Professor Hélio Roberto da Rocha, Mestre em Matemática. |
| Componente Curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0524) Resolver e elaborar situações-problema que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9º ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9° ano – Ensino Fundamental; Matemática; Goiânia, 2024. |
