Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8º Ano do Ensino Fundamental – Anos Finais.

Introdução
Neste texto, exploraremos os conceitos de volume e capacidade aplicados a blocos retangulares, também conhecidos como paralelepípedos. Vamos entender o que são esses conceitos, como calcular o volume de um bloco retangular e a diferença entre volume e capacidade. No final, você encontrará dois problemas para testar seus conhecimentos.
Imagem: canva.com/paralelepípedo
O que é Volume?
O volume de um objeto tridimensional é a quantidade de espaço que ele ocupa. É como se estivéssemos medindo “o tamanho” de um objeto em três dimensões.
O volume é medido em unidades cúbicas, como:
- centímetros cúbicos (cm³),
- decímetros cúbicos (dm³) ou
- metros cúbicos (m³).
O que é Capacidade?
A capacidade está relacionada ao volume interno de um recipiente, ou seja, à quantidade de líquido ou material que um recipiente pode conter.
A capacidade é frequentemente expressa em:
- litros (L) ou
- mililitros (mL).
Relação entre Volume e Capacidade
A capacidade de um recipiente é numericamente igual ao volume do espaço que ele ocupa.
Por exemplo:
- 1 metro cúbico (1m3) tem uma capacidade de 1000 litros.
- 1 centímetro cúbico (cm³) tem uma capacidade de 1 mililitro (1 mL).
- 1 decímetro cúbico (dm³) tem a capacidade de 1000 mililitros (1000mL).
Calculando o Volume de Blocos Retangulares
Existem 2 blocos retangulares bastante comuns nas construções e nos objetos que manuseamos no nosso dia a dia.
São eles:
- Paralelepípedo
- Cubo
O Paralelepípedo é um bloco (sólido geométrico) formado por seis faces retangulares e o seu volume é dado pelo produto das medidas do seu comprimento, da sua largura e da sua altura.
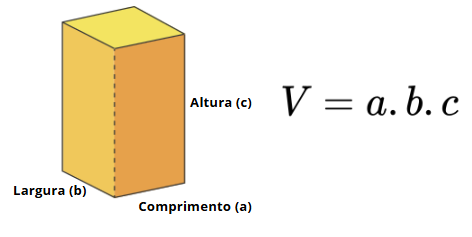
Imagem produzida no canva.com.br
O Cubo é um paralelepípedo especial, onde todas as arestas têm o mesmo comprimento e o seu volume é dado pelo produto de 3 arestas.
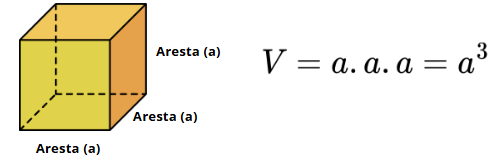
Imagem produzida no canva.com.br
2 Problemas para finalizar
Problema 1: Um bloco retangular tem um comprimento de 10 cm, uma largura de 6 cm e uma altura de 8 cm. Qual é o volume desse bloco?
Resolução:
Utilizando a fórmula do volume dada acima e, já substituindo os valores, temos:
- Volume = 10 cm × 6 cm × 8 cm
- Volume = 480 cm³
Resposta: O volume do bloco retangular é de 480 centímetros cúbicos.
Problema 2: Uma caixa d’água tem a forma de um bloco retangular com comprimento de 1 metro, largura de 0,5 metros e altura de 0,4 metros. Qual é a capacidade dessa caixa em litros?
Resolução:
Utilizando a mesma fórmula do problema 1 e já substituindo os valores, temos:
Volume = 1 m × 0,5 m × 0,4 m = 0,2 m³.
Sabemos que 1 m³ equivale a 1000 litros.
Então, 0,2 m³ são equivalentes a 0,2 . 1000 = 200 litros.
Resposta: A capacidade da caixa d’água é de 200 litros.
Ficamos por aqui, até o próximo.
QUESTÃO 1
Uma caixa de sapatos tem a forma de um bloco retangular. Sabendo que ela mede 30 cm de comprimento, 20 cm de largura e 15 cm de altura, podemos afirmar que o volume dessa caixa é de
(A) 600 cm³.
(B) 9000 cm³.
(C) 12000 cm³.
(D) 15000 cm³.
QUESTÃO 2
Um aquário tem a forma de um bloco retangular e suas dimensões internas são: 60 cm de comprimento, 40 cm de largura e 50 cm de altura. A capacidade total desse aquário, em litros, é de
(A) 120 litros.
(B) 1200 litros.
(C) 12000 litros.
(D) 120000 litros.
QUESTÃO 3
Uma piscina olímpica tem formato de um paralelepípedo reto-retângulo com as seguintes dimensões: 50 metros de comprimento, 25 metros de largura e 2 metros de profundidade.
A) Calcule o volume de água necessário para encher completamente a piscina em metros cúbicos.
B) Sabendo que 1 m³ equivale a 1000 litros, quantos litros de água são necessários para encher a piscina?
QUESTÃO 4
Um bloco de gelo tem a forma de um cubo com aresta medindo 20 cm.
A) Qual é o volume do bloco de gelo em centímetros cúbicos?
B) Se o bloco de gelo derreter completamente, qual será o volume da água obtida? Explique sua resposta.
Aprenda um pouco mais neste vídeo do canal do Prof. Hélio.
| Autoria: | Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA24) Ler, interpretar, resolver e elaborar problemas que envolvam as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas, inseridos, sempre que possível, em contextos oriundos de situações reais e/ou relacionadas às outras áreas do conhecimento. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |
