Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9º Ano do Ensino Fundamental – Anos Finais.
Introdução
As funções quadráticas desempenham um papel fundamental na matemática e em diversas aplicações do mundo real e são encontradas, principalmente, na física e engenharia. Este texto irá abordar a definição de funções quadráticas, a natureza dos gráficos que representam essas funções, a importância dos coeficientes e no final, um problema prático para ilustrar esses conceitos.
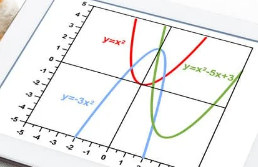
Imagem: canva.com/função_quadrática
Definição de Função Quadrática
Uma função quadrática é uma função polinomial de grau dois, expressa na forma geral
Onde a, b e c são números reais e a diferente de 0, chamados de coeficientes. Cada um desses coeficientes desempenha um papel fundamental na definição da parábola.
A característica principal de uma função quadrática é a presença do termo
que é responsável pela forma parabólica do gráfico.
Tipo de Gráfico da Função Quadrática
O gráfico de uma função quadrática é uma parábola. Ela pode ter duas orientações que irão depender do sinal do coeficiente a.
- Se a for positivo, a parábola se abre para cima, formando um “U” voltado para cima, e
- Se a for negativo, a parábola se abre para baixo, parecendo um “U” invertido.
Imagem do autor produzida no Geogebra
Os coeficientes
O Coeficiente Angular
O coeficiente angular, representado por a na expressão, além de determinar a curvatura e a orientação da parábola, influencia a abertura ou fechamento da parábola. Quanto maior o valor de a, mais fechada será a parábola. Veja na imagem um exemplo:
Imagem do autor produzida no Geogebra
O Coeficiente Linear
O coeficiente linear b influencia a inclinação da parábola e a posição do vértice no eixo horizontal. Embora seu impacto não seja tão visualmente marcante quanto o do coeficiente angular a, ele desempenha um papel crucial em deslocar a parábola ao longo do eixo x.
Imagem do autor produzida no Geogebra
O Termo Independente
O termo independente c é responsável por definir o ponto de interseção da parábola com o eixo y.
Imagem do autor produzida no Geogebra
Um problema de aplicação
A altura h de uma planta em centímetros, após t semanas, é modelada pela função quadrática
Aqui, a=−2, b=8 e c=5. Esses coeficientes indicam que a planta inicialmente cresce, atinge uma altura máxima, e depois começa a diminuir em altura devido a fatores ambientais ou à idade avançada. O que podemos dizer sobre o comportamento da função quadrática com base nesses valores?
Resposta:
- Coeficiente a = -2: indica que a parábola se abre para baixo, indicando que após um certo ponto, a altura da planta começará a diminuir.
- Coeficiente b=8: indica que a taxa de crescimento inicial é positiva, contribuindo para o aumento da altura até atingir o ponto máximo.
- Termo Independente c=5: representa a altura inicial da planta, que é de 5 centímetros quando t=0.
Uma mensagem
Compreender funções quadráticas e seus coeficientes é crucial para resolver problemas práticos e teóricos, como prever a trajetória de um objeto e otimizar o lucro de uma empresa, vale a pena dominar este conceito matemático.
Ficamos por aqui, até o próximo.
QUESTÃO 1
Um projétil é lançado para cima a partir do solo. A altura h (em metros) do projétil em relação ao solo em função do tempo t (em segundos) é dada por
O termo independente dessa função:
(A) representa a altura máxima alcançada pelo projétil.
(B) indica a velocidade inicial do projétil.
(C) representa a altura inicial do projétil.
(D) não possui significado físico nesse contexto.
QUESTÃO 2
Um agricultor deseja cercar um terreno retangular utilizando 100 metros de cerca. Sabendo que a largura do terreno é x metros, a área A (em m²) do terreno em função de x pode ser representada por uma função
(A) do 1º grau.
(B) do 2º grau ou quadrática.
(C) do 3º grau o cúbica.
(D) do 4º grau.
QUESTÃO 3
Um projétil é lançado obliquamente a partir do solo. A altura h (em metros) do projétil em relação ao solo em função da distância horizontal x (em metros) percorrida é dada por
Quais são os valores dos coeficientes a, b e c na função quadrática e o que cada um desses coeficientes indica sobre a trajetória do projétil?
QUESTÃO 4
Uma empresa fabrica caixas de papelão com formato de cubo. O custo de produção C (em reais) de cada caixa em função da medida L (em centímetros) da aresta é dado por
A) Qual o custo de produção de uma caixa com aresta de 10 cm?
B) Se a empresa deseja reduzir o custo de produção de uma caixa, qual variável ela deve modificar e por quê?
| Autoria: | Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA06-D) Reconhecer uma função quadrática e seus coeficientes angular, linear e termo independente quando apresentada em situações problemas diversos. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |
