Matemática – As razões trigonométricas

Esta proposta de atividade de MATEMÁTICA é destinada aos estudante do 6º Período da Educação de Jovens e Adultos–EJA

Definição de razões trigonométricas

Razões trigonométricas são formas de relacionar os ângulos de um triângulo com os comprimentos de seus lados. No caso de um triângulo retângulo, temos três razões principais: 

• Seno (sen)
• Cosseno (cos) 
• Tangente (tan) 

Elas ajudam a calcular distâncias e alturas de objetos que não podemos medir diretamente

A razão seno (sen)

O seno de um ângulo em um triângulo retângulo é a razão entre a medida do cateto oposto ao ângulo e a medida da hipotenusa.

A razão cosseno (cos)

O cosseno de um ângulo é a razão entre entre a medida do cateto adjacente ao ângulo e a medida da hipotenusa.

A razão tangente (tan)

A tangente de um ângulo é a razão entre a medida do cateto oposto ao ângulo e a medida do cateto adjacente.

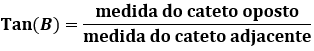
Resumindo

Considerando o triângulo retângulo abaixo, temos:

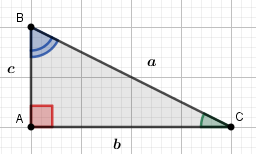
Imagem do autor produzida no Geogebra

As razões trigonométricas para o ângulo B

Para o ângulo B, o cateto oposto é o b e o adjacente é o c.

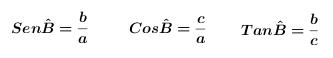
As razões trigonométricas para o ângulo C

Para o ângulo C, o cateto oposto é o c e o adjacente é o b.

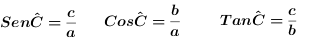
Algumas Aplicações das razões trigonométricas

• Na Arquitetura e Construção: Os arquitetos usam seno, cosseno e tangente para calcular alturas, distâncias e ângulos em projetos de edifícios e outras estruturas.
• Engenharia Civil: Engenheiros civis aplicam trigonometria para projetar estradas, pontes e túneis, calculando inclinações e comprimentos de rampas e viadutos.

Valores mais utilizados das razões trigonométricas

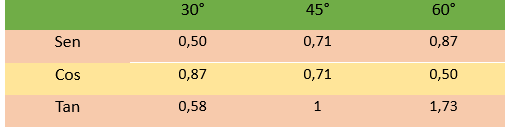
Um problema de aplicação para finalizar

Altura de uma Árvore

Uma pessoa está olhando para o topo de uma árvore a uma distância de 30 metros de sua base. Se o ângulo de elevação ao topo da árvore é de 30°, qual é a altura da árvore?

Graficamente teremos:

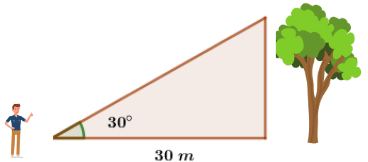
Imagem: canva.com/árvore

Observe que 30m é o cateto adjacente do ângulo de 30° e a medida da altura é o cateto oposto. A razão que relaciona esses dois valores é a tangente. Aplicando a tangente do ângulo de 30° (que é aproximadamente 0,58) e considerando a altura da árvore como h, teremos:

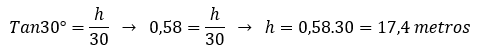
Portanto, a altura da árvore é igual a 17,4 metros.

Ficamos por aqui, até o próximo.

Atividade

QUESTÃO 01

A razão entre o cateto oposto e o cateto adjacente em um triângulo retângulo é conhecida como

(A) cosseno.

(B) seno.

(C) tangente.

(D) secante.

QUESTÃO 02

O seno de um ângulo em um triângulo retângulo é definido como a razão entre

(A) o cateto adjacente e a hipotenusa.

(B) o cateto oposto e a hipotenusa.

(C) os catetos.

(D) a hipotenusa e o cateto oposto.

QUESTÃO 03

Uma escada de 5 metros está encostada em uma parede, formando um ângulo de 60° com o chão. Use o cosseno de 60° (aproximadamente 0,5) para calcular a altura que a escada alcança na parede. Faça um desenho para representar a situação.

QUESTÃO 04

Maria está observando um avião que está diretamente acima de um ponto a 200 metros de distância dela. Se o ângulo de elevação ao avião é de 60°, use a tangente de 60° (aproximadamente 1,73) para calcular a altura do avião em relação ao solo.

Autoria	Professor Hélio Roberto da Rocha, Mestre em matemática
Componente curricular	Matemática
Objetivos de aprendizagem e desenvolvimento	(EJAMA0621) Identificar e diferenciar as razões trigonométricas fundamentais para resolver situações-problema.
Referências	SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6º ao 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024.