Esta proposta de atividade de Matemática é destinada aos estudantes do 5º Período da Educação de Jovens e Adultos – EJA.
Introdução
Neste texto, vou abordar o conceito de números racionais e as operações de raiz quadrada e raiz cúbica aplicadas a esses números. Começarei falando da definição de números racionais, seguido pelas definições e exemplos de raiz quadrada e raiz cúbica. No final, apresentarei duas questões práticas utilizando esses conceitos.
Imagem: canva.com/raiz_https://acesse.one/SAbrm
Números Racionais
Os números racionais são todos os números que podem ser expressos na forma de fração de uma fração.
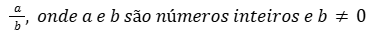
Alguns exemplos:
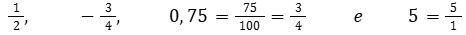
Raiz Quadrada
A raiz quadrada de um número é um valor que, quando multiplicado por si mesmo, resulta no número original.
Em outras palavras, para um número x teremos:
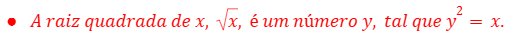
Quando aplicamos a raiz quadrada em números racionais, buscamos um número racional que satisfaz essa condição.
Exemplo de Raiz Quadrada de Números Racionais
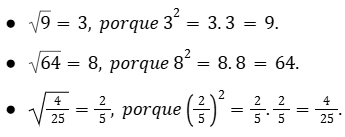
Raiz Cúbica
A raiz cúbica de um número é um valor que, quando multiplicado por si mesmo três vezes, resulta no número original.
Em outras palavras, para um número x teremos:
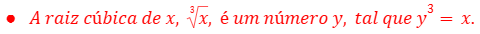
Da mesma forma, ao aplicar a raiz cúbica em números racionais, buscamos um número racional que satisfaça essa condição.
Exemplo de Raiz Cúbica de Números Racionais
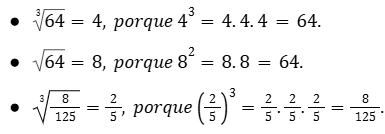
Questões de Aplicação
Questão 1: Raiz Quadrada
Maria quer plantar um jardim quadrado com uma área de 225 metros quadrados. Ela precisa saber o comprimento de um dos lados do jardim para cercá-lo. Qual é a medida das dimensões (largura e comprimento) do lado do jardim?
Resolução:
Lembrando que, em um quadrado, as dimensões (comprimento e largura) tem medidas iguais, logo, para determinar as dimensões do jardim, calculamos a raiz quadrada da área:
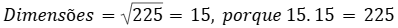
Resposta
As dimensões (largura e comprimento) do jardim são iguais a 15 metros.
Questão 2: Raiz Cúbica
João possui um tanque em forma de cubo com capacidade para 8 metros cúbicos de água. Ele precisa determinar a medida das dimensões (comprimento, largura e altura) desse tanque. Ajude o João!
Resolução
Lembrando que, em um cubo, as dimensões (comprimento, largura e altura) são iguais, logo, para determinar suas dimensões, basta calcular a raiz cúbica do volume:
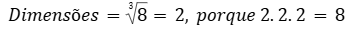
Resposta
As dimensões (largura, comprimento e altura) do tanque são iguais são iguais a 2 metros.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
João está construindo um curral em uma área quadrada de 256 metros quadrados e precisa saber as dimensões desse terreno, para cercar o espaço adequadamente. João pediu ajuda ao seu filho e aplicou os conceitos de área de regiões quadradas e cálculo da raiz quadrada. Após realizar os cálculos, João pode concluir que as dimensões do curral será de
(A) 32 metros de comprimento e 8 metros de largura.
(B) 64 metros de comprimento e 4 metros de largura.
(C) 16 metros de comprimento e 16 metros de largura.
(D) 14 metros de comprimento e 14 metros de largura.
QUESTÃO 02
Podemos afirmar que o valor da expressão numérica, abaixo, é igual a
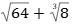
(A) 4.
(B) 6.
(C) 8.
(D) 12.
QUESTÃO 03
João tem um pequeno campo quadrado em sua fazenda onde ele quer plantar flores. Ele sabe que a área do campo é de 144 metros quadrados. Para cercar o campo, ele precisa saber o comprimento de um dos lados. Além disso, ele quer dividir o campo em 9 quadrados menores de tamanhos iguais.
A) Calcule o comprimento de um dos lados do campo original.
B) Após dividir o campo em 9 quadrados menores, determine o comprimento de um dos lados de cada quadrado menor.
QUESTÃO 04
Ana está organizando sua despensa e precisa guardar grãos em caixas cúbicas. Ela tem uma grande caixa cúbica com um volume de 27 metros cúbicos e quer distribuir os grãos em caixas menores, também cúbicas, cada uma com um volume de 1 metro cúbico.
A) Calcule a medida das dimensões (comprimento, largura e altura) da grande caixa cúbica.
B) Determine quantas caixas menores, cada uma com 1 metro cúbico de volume, ela precisará para armazenar todos os grãos da grande caixa.
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0506) Resolver situações-problema com adição, subtração, multiplicação, divisão, potenciação e radiciação (raiz quadrada e cúbica) de números racionais, compreendendo a relação entre elas e suas propriedades operatórias em situações diversas. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ao 9º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6° ao 9º ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. |
