Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 6º Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAGFysRkaRs/rdOZEuohx26Bs_B6P8SiCw/edit?utm_content=DAGFysRkaRs&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 20 de maio de 2024.
O sistema de numeração decimal, também conhecido como sistema Indo-Arábico, é o mais comum no em todo o mundo devido à sua eficiência, simplicidade e flexibilidade. Este sistema utiliza dez símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Esses símbolos são chamados de algarismos e com eles podemos formar infinitos números. As principais características do sistema de numeração decimal incluem a base 10, o valor posicional e a função do zero.
Base 10: O sistema decimal é um sistema de base 10, o que significa que ele usa dez algarismos diferentes (de 0 a 9). Cada posição em um número representa uma potência de 10.
Veja o exemplo do número 345:
A posição do 5 representa:
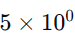
A posição do 4 representa:
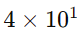
A posição do 3 representa:
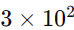
Valor Posicional: O valor posicional é uma característica fundamental do sistema decimal. O valor de um algarismo depende de sua posição no número. Por exemplo, no número 123, o algarismo 1 representa cem unidades (1×100), o algarismo 2 representa vinte unidades (2×10) e o algarismo 3 representa três unidades (3×1).
Função do Zero: O zero é muito importante no sistema de numeração decimal. A maior parte das civilizações antigas não possuíam símbolo para indicar a falta de quantidades. Ele atua como um marcador de posição. Por exemplo, no número 102, o zero indica que não há dezenas. Além disso, o zero representa números nulos.
A relevância do sistema de numeração decimal se torna mais evidente quando comparado a outros sistemas de numeração históricos, como o Egípcio, Babilônico, Romano e Maia.
Sistema Egípcio: O sistema de numeração egípcio era um sistema aditivo que utilizava hieróglifos para representar números. Embora eficiente para representar números pequenos, tornava-se complexo e impraticável para números maiores devido à falta de valor posicional e à ausência de um símbolo para o zero.
Sistema Babilônico: O sistema babilônico era um sistema de base 60, com símbolos cuneiformes representando unidades e dezenas. Apesar de avançado, especialmente em cálculos astronômicos, a falta de um símbolo consistente para o zero e a complexidade da base 60 limitavam sua eficiência em cálculos diários.
Sistema Romano: O sistema de numeração romano utilizava letras do alfabeto para representar valores. Embora adequado para registros históricos e contagens simples, a ausência de valor posicional e de um símbolo para o zero dificultava operações aritméticas complexas.
Sistema Maia: O sistema de numeração maia era um sistema de base 20 que utilizava símbolos para representar unidades e vinte. Embora possuísse um conceito de zero, a base 20 tornava os cálculos mais complexos em comparação ao sistema decimal.
Agora que você , que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Ana tem 3 cartões coloridos com os algarismos 5, 2 e 3. Quais os números de três algarismos diferentes que podem ser formados com esses cartões?
QUESTÃO 2
Carlos ganhou um prêmio de R$ 1.234,56 em um concurso. Determine o valor posicional de cada algarismo nesse número.
QUESTÃO 3
Maria foi à papelaria e comprou materiais escolares que custaram R$ 43,87. O valor posicional do algarismo 8 é
(A) 0,08.
(B) 8.
(C) 0,8.
(D) 80.
QUESTÃO 4
João economizou R$ 5.672,39 durante o ano. O valor posicional do algarismo 7 é
(A) 70.
(B) 7.
(C) 700.
(D) 7000.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA02-E) Estabelecer as principais características do sistema de numeração decimal, Indo-Arábico, como base, valor posicional e função do zero que justifica a sua relevância em comparação aos outros sistemas de numeração, Egípcio, Babilônico, Romano e Maia. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |

