Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 7º Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAGEMRpKqEc/5jMnz5TXTsJIyT9vp4gZ4w/edit?utm_content=DAGEMRpKqEc&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
As sequências recursivas são utilizadas para modelar e descrever padrões e fenômenos naturais. Elas são sequências em que cada termo subsequente é definido em função dos termos anteriores, seguindo uma determinada regra ou padrão.
Uma das sequências recursivas mais simples e importantes é a construção do conjunto dos números naturais. Começamos com o número 0 e, em seguida, adicionamos 1 a cada termo subsequente para obter os números naturais: 0, 1, 2, 3, 4, 5, e assim por diante. Essa sequência é fundamental para a contagem e é a base para muitos outros conceitos matemáticos.
Além disso, as sequências numéricas aditivas e multiplicativas são frequentemente utilizadas para modelar padrões de crescimento e progressão. Na sequência aditiva, cada termo subsequente é obtido pela adição de um número fixo ao termo anterior, enquanto na sequência multiplicativa, cada termo subsequente é obtido pela multiplicação por um número fixo. Por exemplo, a sequência aditiva 2, 4, 6, 8, 10,… é obtida adicionando-se 2 a cada termo subsequente, enquanto a sequência multiplicativa 2, 4, 8, 16,… é obtida multiplicando-se cada termo por 2.
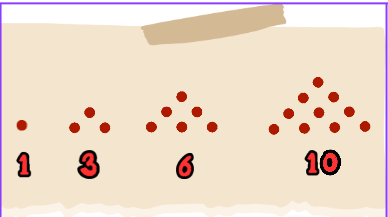
Outro exemplo importante de sequência recursiva é a construção dos números poligonais. Os números poligonais representam o número de pontos que podem ser dispostos para formar polígonos regulares de diferentes formas. Por exemplo, o segundo número triangular é 3, pois podemos formar um triângulo com 3 pontos.
Disponível em: <https://www.canva.com/design/DAGEMRpKqEc/5jMnz5TXTsJIyT9vp4gZ4w/edit?utm_content=DAGEMRpKqEc&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
Por fim, a sequência de Fibonacci é uma das sequências recursivas mais famosas e mais estudadas na matemática. Nesta sequência, cada termo subsequente é a soma dos dois termos anteriores. Começando com 0 e 1, os primeiros termos da sequência de Fibonacci são: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, e assim por diante.

Disponível em: <https://www.canva.com/design/DAGEMRpKqEc/5jMnz5TXTsJIyT9vp4gZ4w/edit?utm_content=DAGEMRpKqEc&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
Esta sequência aparece em muitos contextos naturais, como na disposição de folhas em uma planta, no crescimento populacional de certos organismos e em padrões encontrados em conchas e flores.

Disponível em: <https://www.canva.com/design/DAGEMRpKqEc/5jMnz5TXTsJIyT9vp4gZ4w/edit?utm_content=DAGEMRpKqEc&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
Para exemplificar a aplicação dessas sequências, vamos resolver alguns problemas:
Sequência Aditiva: Se a sequência aditiva 3, 7, 11, 15,… é continuada, qual é o próximo termo?
Solução: Cada termo subsequente é obtido adicionando-se 4 ao termo anterior. Portanto, o próximo termo seria 19.
Sequência Multiplicativa: Na sequência multiplicativa 5, 15, 45, 135,…, qual é o próximo termo?
Solução: Cada termo subsequente é obtido multiplicando-se por 3 o termo anterior. Portanto, o próximo termo seria 405.
Números Poligonais: Qual é o quarto número triangular?
Solução: O quarto número triangular é obtido somando-se os primeiros 4 números naturais: 1 + 2 + 3 + 4 = 10.
Sequência de Fibonacci: Qual é o décimo termo da sequência de Fibonacci?
Solução: A sequência de Fibonacci começa com 0 e 1, e cada termo subsequente é a soma dos dois termos anteriores. O décimo termo seria 34.
QUESTÃO 1
Ana adota um método de estudo em que revisa um novo tópico a cada dia. No primeiro dia, ela estuda um tópico; no segundo dia, dois novos tópicos; no terceiro dia, três novos tópicos, e assim por diante, aumentando em um tópico a cada dia. Se ela começar a estudar na segunda-feira, quantos tópicos ela terá revisado até sexta-feira?
QUESTÃO 2
Maria está cultivando uma planta que cresce 5 centímetros a cada semana. Se hoje a planta tem 20 centímetros de altura, após mais duas semanas ela terá
(A) 30 cm.
(B) 35 cm.
(C) 40 cm.
(D) 45 cm.
QUESTÃO 3
Uma sequência de números é formada por quadrados perfeitos: 1, 4, 9, 16, 25, … O próximo número na sequência é
(A) 36.
(B) 49.
(C) 64.
(D) 81.
QUESTÃO 4
Pedro está aprendendo a tocar guitarra e pratica um novo acorde a cada dia. No primeiro dia, ele aprende um acorde; no segundo dia, dois novos acordes; no terceiro dia, três novos acordes, e assim por diante, aumentando em um acorde a cada dia. Se ele começar a praticar no domingo, quantos acordes ele terá aprendido quando chegar o próximo sábado?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA14-A) Explorar e relacionar diferentes sequências recursivas em situações como a construção do conjunto dos números naturais, a construção de sequências numéricas aditivas e multiplicativas, a construção dos números poligonais e a construção da sequência de Fibonacci. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |

