Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 6º Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAGD0nLnKWc/z9nXMUDJKZwW4amIQoNB-g/edit?utm_content=DAGD0nLnKWc&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de abril de 2024.
Múltiplos são números resultantes da multiplicação de um número inteiro por outro. Em outras palavras, um múltiplo de um número é qualquer número que possa ser expresso como o produto desse número por todos os outros. Por exemplo, os múltiplos de 3 são 0, 3, 6, 9, 12, 15 e assim por diante, porque cada um desses números pode ser obtido multiplicando-se 3 por um número diferente. Todos os números têm infinitos múltiplos, pois podemos multiplicar qualquer número por qualquer outro número para obter um novo múltiplo.
O Mínimo Múltiplo Comum (MMC) é o menor múltiplo comum a dois ou mais números inteiros. É útil em situações que envolvem frações, simplificação de frações, operações com frações e resolução de equações.
Resolução pela sequência dos múltiplos:
Para calcular o MMC, existem diferentes métodos, primeiro faremos determinando a sequência de múltiplos de cada número e identificando o primeiro múltiplo em comum, que não seja o zero. Veja:
Exemplo: Ana e João são dois amigos que estão participando de uma competição de quebra-cabeças. Ana resolve um quebra-cabeça a cada 6 minutos, enquanto João resolve um quebra-cabeça a cada 9 minutos. Eles começam a resolver os quebra-cabeças ao mesmo tempo. Em quantos minutos eles resolverão um quebra-cabeça juntos novamente?
Solução:
Vamos encontrar os múltiplos de 6 e 9 até que encontremos um múltiplo comum.
Múltiplos de 6: {0, 6, 12, 18, 24, 30, 36, …}
Múltiplos de 9: {0, 9, 18, 27, 36, …}
Aqui vemos que o primeiro número em comum é 18 (excluindo o zero). Isso significa que Ana e João resolverão um quebra-cabeça juntos novamente após 18 minutos.
Método da decomposição em fatores primos:
Um dos mais utilizados é o método de decomposição em fatores primos. Vou explicar esse método usando um exemplo:
Exemplo: Maria precisa comprar materiais para fazer artesanato. Ela precisa de tinta a cada 15 dias e de cola a cada 20 dias. Em quantos dias ela precisará comprar tanto tinta quanto cola novamente?
Solução:
Vamos começar decompondo 15 e 20 em seus fatores primos. Em seguida multiplicamos esses fatores:
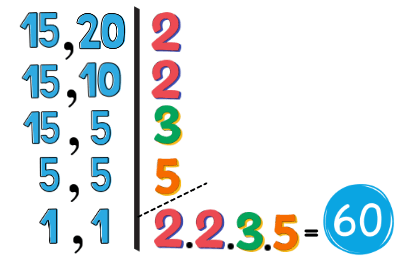
Resposta: Maria precisará comprar tanto tinta quanto cola novamente a cada 60 dias.
Agora que você aprendeu a calcular o mmc de duas formas diferentes, que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Maria tem um jardim onde precisa regar as plantas a cada 4 dias e cortar a grama a cada 6 dias. Ela precisará realizar ambas as tarefas novamente em
(A) 8 dias.
(B) 10 dias.
(C) 12 dias.
(D) 14 dias.
QUESTÃO 2
Um grupo de amigos gosta de jogar futebol e basquete. Eles jogam futebol a cada 5 dias e basquete a cada 10 dias. Eles poderão organizar uma partida de futebol e basquete no mesmo dia a cada
(A) 10 dias.
(B) 15 dias.
(C) 20 dias.
(D) 25 dias.
QUESTÃO 3
Uma fábrica produz bicicletas a cada 15 dias e skates a cada 12 dias. Daqui a quantos dias ela terá que iniciar a produção de ambos os produtos simultaneamente?
QUESTÃO 4
João precisa revisar suas aulas de inglês a cada 9 dias e suas aulas de matemática a cada 12 dias. Em quantos dias ele precisará revisar ambas as matérias no mesmo dia?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA06-A) Reconhecer e compreender o Mínimo Múltiplo Comum entre pelo menos dois números naturais. (EF06MA06-B) Estabelecer e construir estratégias para determinar o Mínimo Múltiplo Comum entre pelo menos dois números naturais. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |
