Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 9° Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAF8-k6ZBAw/-TRUIPdksrb_T2IDrN0Y_A/edit?utm_content=DAF8-k6ZBAw&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 20 de abril de 2024.
Os números irracionais são de grande importância na geometria e nas medidas, pois representam grandezas que não podem ser expressas como frações de números inteiros.
Um dos números irracionais mais conhecidos é o pi (π), que representa a razão entre a circunferência de um círculo e seu diâmetro. Embora seja impossível expressar π como uma fração com numerador e denominador inteiros, ele é importante em diversos cálculos geométricos, como o cálculo de áreas e volumes de figuras circulares. Por exemplo, a área de um círculo é dada pela fórmula A = πr², onde r é o raio do círculo. circulares.
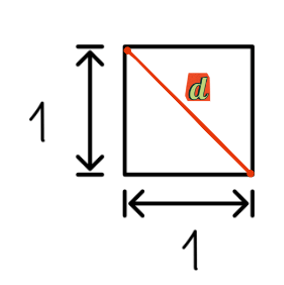
Outro exemplo de números irracionais na geometria são as raízes quadradas de números não quadrados perfeitos, como √2 e √3. Esses números aparecem em muitos contextos geométricos, como o comprimento da diagonal de um quadrado unitário ou o lado de um triângulo equilátero inscrito em um círculo unitário.
Além disso, os números irracionais são frequentemente encontrados em construções geométricas e em problemas de congruência e semelhança de figuras. Por exemplo, ao dividir um segmento de reta em partes proporcionais, é comum obter medidas irracionais que não podem ser representadas por números racionais. Essas construções são importantes na resolução de problemas geométricos avançados e na demonstração de teoremas fundamentais.
Para ilustrar a aplicação dos números irracionais na geometria, consideremos o seguinte exemplo:
Exemplo: Um triângulo equilátero tem lado de comprimento 5 cm. Calcule a medida da altura desse triângulo sabendo que a altura de um triângulo equilátero é dada por:
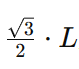
Sendo L a medida do lado do triângulo.
Resolução: Substituindo L = 5, temos:
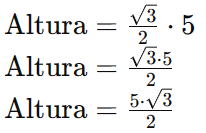
Que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
João está construindo uma pirâmide com uma base triangular equilátera. Ele precisa saber a altura exata de cada face para garantir que a pirâmide tenha a forma correta e seja estável. Se o comprimento do lado dessa base é 8 cm, então a medida da altura é
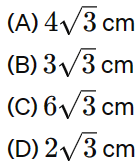
QUESTÃO 2
Maria está planejando pintar o fundo de um barril para usá-lo como um pequeno lago decorativo em seu jardim. Para calcular a quantidade de tinta necessária, ela precisa saber a área da base do barril, que é circular. Como o raio dessa base é 10 cm, então a área é
(A) 25π cm²
(B) 100π cm²
(C) 50π cm²
(D) 10π cm²
QUESTÃO 3
Pedro está decorando um bolo circular para uma festa com raio de 30cm. Qual é a área desse bolo?
QUESTÃO 4
Ana está planejando cercar um jardim quadrado com uma cerca decorativa. Para comprar a quantidade certa de material, ela precisa saber o comprimento total da cerca. Ela sabe que a área do jardim mede 36√2 m², então, qual é o perímetro?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF09MA01-A) Compreender que existem problemas, especialmente alguns vinculados à geometria e medidas, cujas soluções não são dadas por números racionais (caso do π, da √2, √3 etc.). |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |
