Esta proposta de atividade de Matemática com base no DC/GO – Ampliado e é destinada aos estudantes do 8° Ano do Ensino Fundamental – Anos Finais.

Disponível em: <https://www.canva.com/design/DAF8-k6ZBAw/-TRUIPdksrb_T2IDrN0Y_A/edit?utm_content=DAF8-k6ZBAw&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton> último acesso em 30 de março de 2024.
O cálculo de porcentagens é importante na educação financeira, pois capacita as pessoas a resolver problemas com questões envolvendo finanças do dia a dia.
Ao dominar o conceito de porcentagem, podemos calcular descontos em compras, comparar taxas de juros em empréstimos ou investimentos, entender a variação de preços ao longo do tempo e avaliar o impacto de diferentes opções financeiras. Além de evitar gastos desnecessários e dívidas excessivas, estudar esse assunto também possibilita o planejamento para alcançar metas financeiras, como economizar para aposentadoria, fazer uma viagem ou adquirir bens de maior valor.
Ao compreender como os descontos e as taxas percentuais afetam o preço final de um produto, as pessoas podem avaliar se uma oferta é realmente vantajosa e se estão obtendo o melhor valor pelo seu dinheiro. Isso é especialmente importante em um cenário de compras parceladas, onde os consumidores podem ser facilmente influenciados pelo valor aparentemente baixo das parcelas, sem considerar o custo total do produto.
Nesse contexto, o uso de tecnologias digitais, como aplicativos de celular, softwares e ferramentas online, podem nos auxiliar a realizar cálculos e comparativos de forma simples para tomar decisões financeiras mais eficientes.
Dessa forma, os consumidores podem tomar decisões mais conscientes, evitando pagar valores absurdos por produtos que podem parecer acessíveis a curto prazo, mas se tornam onerosos a longo prazo devido a juros e encargos adicionais.
Cálculo de porcentagem:
Podemos fazer o cálculo de porcentagens usando multiplicação de frações com denominador 100 e usando a multiplicação com números decimais, que agiliza o processo quando temos calculadora disponível.
Veja os exemplos:
Exemplo 1: Ana está fazendo compras em uma loja que oferece descontos progressivos. Se ela compra 3 itens iguais, recebe 10% de desconto; se compra 4 itens iguais, recebe 15% de desconto; e se compra 7 itens ou mais, recebe 20% de desconto. Como Ana comprou 4 blusas de R$ 45,50 cada e 3 calças de R$ 120,00, qual foi o valor total do desconto que Ana recebeu?
Resolução:
1°) Cálculo do valor total:
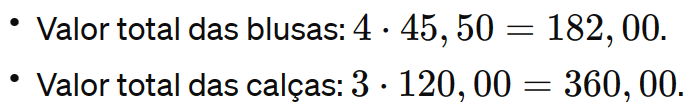
2°) Aplicar os descontos nos itens:
Como Ana comprou 4 itens (4 blusas), ela recebe um desconto de 15%:
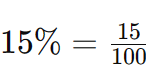
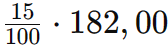
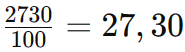
Portanto, o desconto das blusas é de R$ 27,30. Agora vamos calcular o valor do desconto das calças:
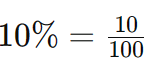
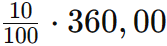
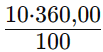
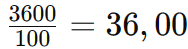
3°) Calcular o valor total do desconto:
Agora que já calculamos o desconto das blusas e das calças, precisamos somar esses valores para encontrar o valor total do desconto que Ana recebeu.
Portanto, o valor total do desconto que Ana recebeu é de
R$ 27,30 (blusas) + R$ 36,00 (calças) = R$ 63,30.
Exemplo 2: Uma cidade tinha uma população de 500.000 habitantes em 2020. Em 2021, houve uma redução de 15% na população devido à migração. Quantos habitantes a cidade tinha em 2021?
Resolução:
Podemos representar a porcentagem na forma de número decimal:
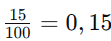
Esse valor corresponde à redução, então os habitantes restantes correspondem a 0,85:
0,85 . 500 000 = 425 000 habitantes
Agora que você aprendeu sobre porcentagem, que tal fazer uma atividade para testar seus conhecimentos?
QUESTÃO 1
Em uma pesquisa sobre preferência de filmes, 40% dos entrevistados escolheram filmes de ação, 30% preferiram filmes de comédia e o restante optou por outros gêneros. Se 120 pessoas foram entrevistadas, quantas escolheram filmes de outros gêneros?
(A) 24
(B) 36
(C) 48
(D) 60
Questão 2
João está planejando comprar um novo celular e encontra duas lojas diferentes, A e B, que oferecem descontos diferentes no mesmo modelo de celular. Na loja A, o celular está com 20% de desconto sobre o preço original de R$ 1500,00. Na loja B, o mesmo modelo de celular está com 15% de desconto sobre o preço original de R$ 1600,00. Ao fazer os cálculos, João percebeu que
(A) Era mais vantajoso comprar na loja A, pois pagaria um valor de R$ 1200,00 pelo celular, enquanto na loja B ele pagaria um valor de R$ 1360,00.
(B) Era mais vantajoso comprar na loja B, pois pagaria um valor de R$ 1360,00 pelo celular, enquanto na loja A ele pagaria um valor de R$ 1200,00.
(C) Não havia diferença significativa entre os preços das lojas A e B, já que ambos os descontos resultavam em valores de compra semelhantes.
(D) Era impossível determinar qual loja oferecia a compra mais lucrativa sem saber o valor final do desconto em cada loja.
QUESTÃO 3
Ana está comprando roupas em uma loja que oferece descontos progressivos. Se ela comprar 3 peças idênticas, recebe um desconto de 10%; se comprar 4 peças idênticas, recebe 15% de desconto; e se comprar 6 peças ou mais, recebe 20% de desconto. Ana comprou 5 camisetas da mesma marca por 56 reais cada. Qual é o valor final da compra de Ana?
QUESTÃO 4
Maria fez uma prova com 50 questões. Ela ganha 2 pontos para cada resposta correta e perde 1 ponto para cada resposta errada. Sabendo que Maria acertou 80% das questões? Qual foi a sua nota?
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF08MA04-B) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais, no contexto da educação financeira. |
| Referências | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 23/03/2024. |

