ESTA PROPOSTA DE ATIVIDADE DE MATEMÁTICA É DESTINADA AOS ESTUDANTES DO 3º ANO DO ENSINO FUNDAMENTAL.
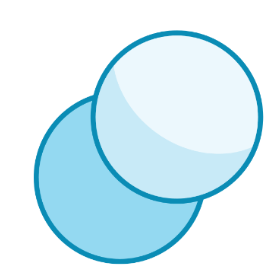
Superposição de áreas
O que são áreas?
Para começar, vamos entender o que é uma área. Área é a medida da superfície de uma figura ou objeto. É como se fosse o espaço ocupado por ela. Por exemplo, quando olhamos para um retângulo, a área nos diz quanto espaço essa forma ocupa em uma superfície plana.
Comparando áreas: visualmente e por superposição
Agora, vamos falar sobre como podemos comparar áreas. Existem duas maneiras principais de fazer isso: visualmente e por superposição.
Visualmente: Quando comparamos áreas visualmente, estamos usando nossos olhos para observar e julgar. Por exemplo, se temos dois retângulos de tamanhos diferentes, podemos comparar suas áreas olhando para eles e percebendo qual parece ser maior ou menor. É como dizer “este retângulo parece ocupar mais espaço do que aquele”.
Por superposição: Por outro lado, quando comparamos áreas por superposição, estamos literalmente sobrepondo uma figura sobre a outra para ver como elas se encaixam. Por exemplo, se temos um quadrado e um retângulo, podemos sobrepor o quadrado sobre o retângulo e ver se ele cobre toda a área do retângulo ou se sobra algum espaço. Se o quadrado cobrir completamente o retângulo, significa que suas áreas são iguais. Se sobrar algum espaço, isso nos mostra que uma das áreas é maior que a outra.
Por que é importante comparar áreas?
Comparar áreas é útil em muitas situações da vida real. Por exemplo, quando você está organizando livros em uma prateleira, é importante saber qual livro é maior para garantir que eles se encaixem corretamente. Além disso, entender áreas nos ajuda a resolver problemas de matemática, como calcular a quantidade de tinta necessária para pintar uma parede ou a área de um terreno.
QUESTÃO 1
Considere dois retângulos com dimensões diferentes. Explique como você pode determinar, através da comparação visual e por superposição, qual retângulo tem a maior área. Descreva passo a passo os métodos utilizados e forneça uma justificativa matemática para sua conclusão.
QUESTÃO 2
Suponha que você tenha um terreno retangular e deseje construir uma piscina circular nele. Como você pode determinar se a piscina caberá no terreno? Desenvolva um raciocínio matemático que envolva a comparação das áreas do terreno e da piscina, tanto visualmente quanto por superposição. Explique como essa habilidade matemática pode ser útil na prática e forneça uma conclusão baseada em seus cálculos.
QUESTÃO 3
Lucas tinha uma quantia desconhecida de dinheiro. Ele gastou 45 reais comprando brinquedos e depois encontrou 20 reais no bolso de sua mochila. Agora, Lucas tem 55 reais. Lucas tinha inicialmente
(A) 80 reais.
(B) 90 reais.
(C) 100 reais.
(D) 110 reais.
QUESTÃO 4
Para determinar se um círculo pode ser totalmente contido dentro de um quadrado, o método mais eficiente será
(A) comparação por adição.
(B) comparação por subtração.
(C) comparação por superposição.
(D) comparação por visualização direta.
| Autoria: | Lucyana Oliveira Borba |
| Formação: | Pedagogia |
| Componente Curricular: | Matemática |
| Habilidades: | (EF03MA21) Comparar, visualmente ou por superposição, áreas de faces de objetos, de figuras planas ou de desenhos. |
| Referências: | BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2018. CADERNO APRENDER SEMPRE – 1º Bimestre 2024 – 3ºAno/ Ensino Fundamental/ Língua Portuguesa e Matemática/ Prefeitura de Goiânia- Secretaria Municipal de Educação. Documento Curricular para Goiás (DC-GO). Goiânia/GO: CONSED/ UNDIME Goiás, 2018. Disponível em: <https://cutt.ly/MOsX7AS> acessado em 26, jan. 22. |