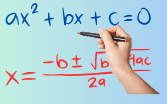Esta proposta de atividade de Matemática é destinada aos estudantes do 6º Período (8ª série) da Educação de Jovens e Adultos – EJA.
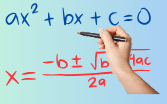
O que são equações?
Uma equação é uma igualdade entre duas sentenças matemáticas contendo uma ou mais incógnitas, representadas geralmente por letras. Elas podem ser resolvidas por meio de operações matemáticas onde se procura determinar os valores que tornam a sentença verdadeira.
Imagem: canva.com/equação
Qual a definição de equação do 2º grau?
São todas as equações algébricas que envolvem uma variável elevada ao quadrado (2º grau), como por exemplo:

Onde:
- a, b e c são números reais, com a diferente de zero, chamados de coeficientes;
- x é a variável que queremos encontrar.
O objetivo é encontrar os valores de x que satisfazem a equação, ou seja, encontrar as raízes da equação.
Quais são os métodos para resolver uma equação do 2º grau?
Alguns deles:
- Fórmula de Bhaskara.
- Soma e produto das raízes.
- Completando quadrado.
- Fatoração.
Neste texto iremos abordar a soma e o produto das raízes.
Soma e Produto das raízes da equação do 2º grau.
Considerando uma equação do 2º grau na forma ax² + bx + c = 0, cujas raízes são representadas por x₁ e x₂, teremos:
- a soma das raízes (S):
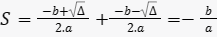
- o produto das raízes (P):
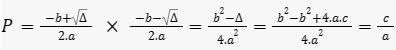
Dividindo a equação ax² + bx + c = 0 por a, obtemos:
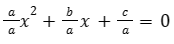
Substituindo os valores S e P, podemos reescrever a equação ax² + bx + c = 0 utilizando a soma (S) e o produto (P) das raízes como:

Veja o vídeo abaixo com essa explicação.
Mas como utilizar esse método para resolver uma equação?
Segue 3 exemplos.
Exemplo 1
Determinar a solução da equação

Vamos comparar essa equação com aquela que aparece a soma e o produto.


Podemos ver, facilmente, que a soma das raízes é igual a 5 e o produto é igual a 6.
Os dois números cuja soma é 5 e produto 6 são as raízes dessa equação.
Esses números são o 2 e o 3 pois 2+3=5 e 2.3=6, logo a solução da equação será S={2,3}.
Exemplo 2:
Determinar o conjunto solução da equação
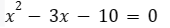
Neste exemplo vamos determinar a soma e o produto através das suas fórmulas.
Os coeficientes da equação são: a = 1, b = -3 e c = -10.
Substituindo esses valores nas fórmulas, obtemos os valores de S e P.
S = -b/a = -(-3)/1 = 3
P = c/a = -10/1 = -10
Temos que determinar 2 números cuja soma seja igual a 3 e cujo produto seja igual a -10.
Facilmente verificamos que esses números são o – 2 e 5 pois, -2+5=3 e (-2).5=-10.
Portanto, a solução da equação é igual a S={-2,5}.
Exemplo 3
Faça o mesmo para a equação
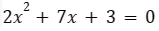
Observe que o valor do coeficiente a é 2 (diferente de 1) então a soma e o produto podem ser números fracionários, neste caso sim. Veja:
Soma das raízes (S) = -b/a = -7/2
Produto das raízes (P) = c/a = 3/2
Agora percebe que fica bem mais complicado determinar as raízes?
Melhor partir para outro método.
No saiba mais temos vídeo explicando.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
A equação do 2º grau que tem o produto das raízes igual a -8 e a soma igual a 4 é dada por:

QUESTÃO 02
Determine a soma e o produto das raízes da equação do 2° grau abaixo.
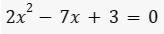
QUESTÃO 03
Um agricultor está planejando construir um campo de futebol retangular em um terreno disponível. Se a largura do campo é metade do comprimento e a área total do campo é de 450 metros quadrados, podemos afirmar que o campo possui
(A) 30 m de comprimento e 15m de largura.
(B) 25m de comprimento e 20m de largura.
(C) 20m de comprimento e 10m de largura.
(D) 15m de comprimento e 7,5m de largura.
QUESTÃO 04
Considere a equação do segundo grau abaixo. Calcule as raízes dessa equação utilizando a soma e o produto das raízes.
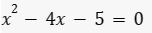
SAIBA MAIS
| Autoria | Professor Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Objetivos de Aprendizagem e Desenvolvimento: | (EJAMA0611) Investigar, por meio de possíveis raízes inteiras com soma S e produto P, as soluções de equações do 2° grau que podem ser comparadas à forma x² – Sx + P = 0. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. |