Esta atividade de Matemática tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 6º ano do Ensino Fundamental.

Disponível em: <Dados Oportunidade Jogatina – Foto gratuita no Pixabay > Acesso em 17 de agosto de 2022.
Contagem e probabilidade são conceitos fundamentais em matemática. Esses temas estão presentes em nosso dia a dia de maneira mais frequente do que imaginamos. Desde a contagem de objetos até a análise de chances e possibilidades, a compreensão desses conceitos ajuda a desenvolver várias habilidades.
A contagem é o processo de determinar quantos elementos há em um conjunto. Pode ser tão simples quanto contar objetos físicos, como lápis ou maçãs, ou mais complexo, envolvendo o número de maneiras diferentes de organizar um grupo de elementos.
Por exemplo, se quisermos contar quantas maçãs temos em uma cesta, basta contar uma por uma. Se temos 5 maçãs, a contagem é direta. No entanto, se quisermos contar quantas maneiras diferentes há de organizar três livros em uma prateleira, precisamos usar princípios de contagem, como a permutação.
Probabilidade:
A probabilidade é uma medida numérica que expressa a chance de um evento ocorrer. Essa medida pode ser representada de diferentes formas, incluindo fração, decimal e porcentagem.
- Forma Fracionária: Na forma fracionária, a probabilidade é expressa como uma fração em que o numerador representa o número de resultados favoráveis e o denominador representa o número total de resultados possíveis. Por exemplo, se a probabilidade de tirar uma bola vermelha de uma caixa é de 2/5, isso significa que existem 2 bolas vermelhas em um total de 5 bolas na caixa.
- Forma Decimal: Na forma decimal, a probabilidade é representada como um número decimal entre 0 e 1, onde 0 indica uma probabilidade nula (evento impossível) e 1 indica uma probabilidade total (evento certo).Utilizando o exemplo anterior, a probabilidade de tirar uma bola vermelha da caixa também pode ser expressa como 0.4 em forma decimal.
- Forma de Porcentagem: Na forma de porcentagem, a probabilidade é representada como uma porcentagem entre 0% e 100%, onde 0% indica uma probabilidade nula e 100% indica uma probabilidade total. Continuando com o exemplo das bolas, a probabilidade de tirar uma bola vermelha da caixa pode ser representada como 40% em forma de porcentagem.
Assista a videoaula da professora Priscilla com essa temática
Vamos responder algumas questões
Questão 1
Maria vai a um evento e tem disponíveis 2 calças (azul e preta) , 4 blusas (vermelha, azul, roxa e rosa) e 2 pares de calçados (sandália e tênis). Copie e complete a tabela e descubra quantas e quais as possibilidades diferentes ela tem de se vestir usando uma calça, uma blusa e um calçado:
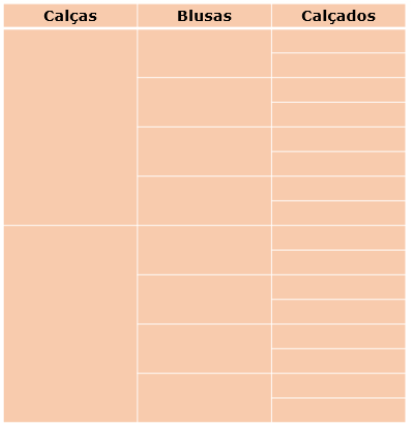
Imagem do arquivo pessoal
Existe outra forma de calcular o total de possibilidades? Qual?
Questão 2
Imagine o lançamento simultâneo de duas moedas e responda:
- Quais são os resultados possíveis?
- Quantos são esses resultados?
- Qual a probabilidade nesse lançamento de obter uma moeda com CARA e a outra com COROA?
- Qual a probabilidade de obter pelo menos uma moeda com face CARA?
Questão 3
Em uma caixa de lápis, há 8 lápis azuis, 5 lápis vermelhos e 3 lápis verdes. A probabilidade de escolher um lápis azul ao acaso é
(A) 40%
(B) 50%
(C) 30%
(D) 20%
Questão 4
Em uma cesta de frutas, há 4 maçãs vermelhas, 2 maçãs verdes e 3 bananas. Se uma fruta for escolhida aleatoriamente, a probabilidade de ser uma banana é
(A) 30%
(B) 25%
(C) 40%
(D) 20%
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF05MA09-A) Ler, interpretar, resolver, analisar e elaborar problemas simples de contagem envolvendo o princípio multiplicativo, como a determinação do número de agrupamentos possíveis ao se combinar cada elemento de uma coleção com todos os elementos de outra coleção, por meio de diagramas de árvore ou por tabelas. (EF06MA30-A) Realizar experimentos aleatórios simples ou simulações que envolvam o cálculo ou a estimativa de probabilidades. (EF06MA30-B) Calcular a probabilidade de um evento aleatório simples, expressando-a por número racional, forma fracionária, decimal e percentual, bem como comparar esse número com a probabilidade obtida por meio de experimentos sucessivos. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6° ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. GOIÁS. Documento Curricular para Goiás – Ampliado. Volume II. Ensino Fundamental Anos Finais. CONSED; UNDIME, 2018. 433 p. Disponível em <https://sme.goiania.go.gov.br/site/index.php/institucional/documentos-oficiais-2/category/27-documentos-gerais>>. Acesso em 11/03/2024. |
