Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.
Disponível em: <Bambu Barreira Tela De Cerca Papel – Foto gratuita no Pixabay> Acesso em 05 de novembro de 2022.
O Teorema de Tales é uma das pedras fundamentais da geometria, mas sua história remonta a um homem cujo legado transcendeu os séculos. Tales de Mileto, frequentemente considerado o primeiro filósofo da tradição ocidental, viveu no século VI a.C., na antiga cidade grega de Mileto, na costa oeste da Ásia Menor, que hoje faz parte da Turquia. Embora muitos detalhes de sua vida tenham sido perdidos para o tempo, suas contribuições para a matemática, astronomia e filosofia moldaram o curso do pensamento humano.
Tales era um homem notável em muitos aspectos. Ele foi um dos Sete Sábios da Grécia Antiga, um grupo de filósofos, legisladores e estadistas famosos por suas máximas e preceitos éticos. Tales viajou extensivamente, absorvendo conhecimento e experiências que o ajudaram a desenvolver suas teorias. Ele era conhecido por sua curiosidade insaciável e sua busca pelo conhecimento.
Uma das contribuições mais duradouras de Tales foi sua compreensão da geometria e seu famoso teorema que leva seu nome. O Teorema de Tales estabelece uma relação entre as medidas dos lados de dois triângulos semelhantes e é fundamental para a resolução de muitos problemas geométricos.
O teorema pode ser expresso da seguinte maneira: Duas retas transversais são interceptadas por um conjunto de retas paralelas, resultando em segmentos proporcionais.
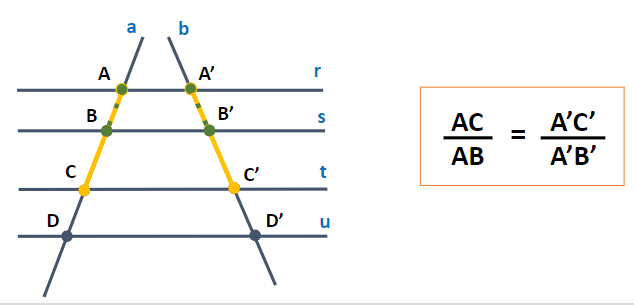
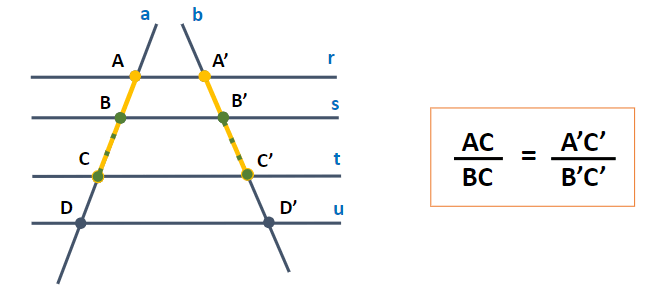
Essa descoberta revolucionou a geometria e teve aplicações em diversas áreas, desde a cartografia até a engenharia. Tales, através de seu teorema, forneceu uma ferramenta poderosa para medir distâncias e calcular áreas, contribuindo assim para o avanço do conhecimento matemático e científico.
O legado de Tales vai além de suas contribuições para a matemática. Ele também foi um pensador influente em questões filosóficas e científicas. Por exemplo, Tales foi um dos primeiros a tentar explicar a natureza do mundo sem recorrer a explicações míticas. Ele propôs que a água era o elemento primordial de todas as coisas, uma teoria que pode ser considerada uma tentativa inicial de explicar a origem e a essência da matéria.
Além disso, Tales também é creditado por prever um eclipse solar em 585 a.C., mostrando sua compreensão da astronomia e seu desejo de entender os padrões e fenômenos naturais.
O Teorema de Tales e as ideias de Tales de Mileto continuam a influenciar o pensamento e a prática científica até os dias de hoje. Sua abordagem racional e investigativa para compreender o mundo ao nosso redor estabeleceu um precedente para a ciência e a filosofia que ainda ressoa nos esforços humanos para descobrir e compreender a verdade. Tales de Mileto, um homem que viveu há milênios, permanece como um farol do conhecimento humano, lembrando-nos da importância da curiosidade e do pensamento crítico na busca pelo entendimento do universo.
Assista a videoaula da professora Priscilla com essa temática.
Questão 1
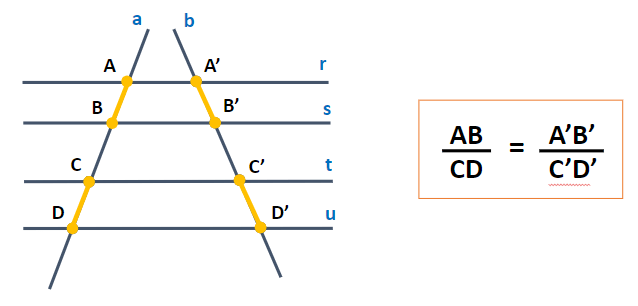
Duas avenidas partem de um mesmo ponto A e cortam duas ruas paralelas. Se na primeira avenida, os quarteirões determinados pelas ruas paralelas medem 80 m e 90 m de comprimento, respectivamente e na segunda avenida, um dos quarteirões determinados mede 60 m, podemos afirmar que o comprimento do outro quarteirão mede
Imagem produzida no canva.com
(A) 54 metros.
(B) 64 metros.
(C) 72 metros.
(D) 80 metros.
Questão 2
Se em uma cidade, duas avenidas partem de um mesmo ponto A e cortam duas ruas paralelas, sendo que na primeira avenida um dos quarteirões determinados mede 70 metros, e na segunda avenida, os quarteirões determinados medem 50 metros e 60 metros, respectivamente, então, podemos afirmar que o comprimento do outro quarteirão da segunda avenida tem
(A) 36 metros.
(B) 40 metros.
(C) 45 metros.
(D) 48 metros.
Questão 3
Sabendo que as retas r, s e t são paralelas, determine o valor de x na imagem a seguir.
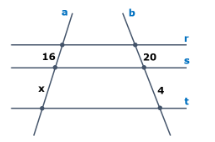
Imagem do autor
Questão 4
Como o Teorema de Tales é aplicado na prática, tanto na matemática quanto em outras áreas?
| Autoria | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades estruturantes: | (EF09MA14-A) Estabelecer o Teorema de Tales, por meio das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes, para calcular distâncias inacessíveis e nas relações envolvendo semelhança de triângulos em problemas diversos. |
| Referências: | GOIÂNIA. Secretaria Municipal de Educação. Aprender sempre. 9°. Ano – Ensino Fundamental; Língua Portuguesa e Matemática; 4°. Bimestre; Goiânia, 2022. |