Esta atividade de Matemática tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 6º ano do Ensino Fundamental.

Disponível em: < Pizza Comida Refeição – Gráfico vetorial grátis no Pixabay> Acesso em 15 de agosto de 2022.
Os números fracionários desempenham um papel fundamental em muitas situações cotidianas, permeando diversos aspectos da vida. Um exemplo notável é a presença marcante de frações em receitas culinárias, onde as medidas precisas são essenciais para o sucesso na preparação de pratos. Essa aplicação prática evidencia como os números fracionários são indispensáveis em atividades rotineiras.
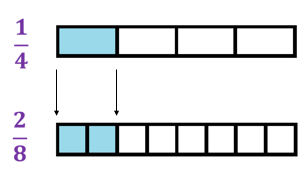
No contexto das frações, é relevante explorar o conceito de equivalência. Duas frações são consideradas equivalentes quando representam a mesma quantidade, mesmo que seus numeradores e denominadores sejam diferentes. Esse conceito é crucial para simplificar e comparar frações, facilitando o entendimento e a manipulação desses números.
Ao analisar as frações em profundidade, observa-se a distinção entre frações próprias e impróprias. Frações próprias são aquelas em que o numerador é menor que o denominador, representando uma quantidade menor que um inteiro. Por exemplo, 1/2 ou 3/4 são frações próprias comumente encontradas em contextos diversos.
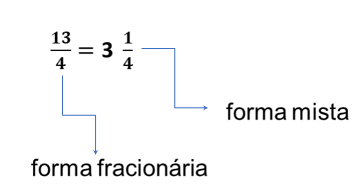
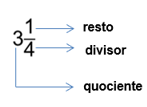
Por outro lado, as frações impróprias representam quantidades que excedem um inteiro. Isso ocorre quando o numerador é maior ou igual ao denominador. Um exemplo prático é a fração13/4, que é maior que 1 e, portanto, classificada como uma fração imprópria. Elas podem ser representadas na forma de número misto:
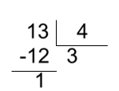
As aplicações de frações vão além do ambiente culinário. Ela se estende para várias áreas, como finanças, ciências e engenharia. Na resolução de problemas do dia a dia, a capacidade de calcular e comparar frações é valiosa. Por exemplo, ao planejar orçamentos financeiros, a habilidade de lidar com frações é essencial para distribuir recursos de maneira eficaz.
Além disso, as frações são frequentemente encontradas em situações que envolvem medidas, como em construções, projetos arquitetônicos e escalas de mapas.
Em resumo, os números fracionários desempenham um papel crucial em várias esferas da vida cotidiana. Desde a cozinha até as aplicações mais complexas em campos profissionais, as frações são ferramentas matemáticas essenciais. A compreensão de conceitos como equivalência, frações próprias e impróprias é fundamental para desenvolver habilidades matemáticas sólidas e aplicá-las de maneira eficaz em diferentes contextos.
Assista a videoaula da professora Priscilla com essa temática
Vamos responder algumas questões
Questão 1
Paulo fez uma torta para seus filhos e João comeu 1/4 dela. Aline comeu 2/8 da torta. Qual dos irmãos comeu mais? Represente essa situação usando desenhos.
Questão 2
Desenhe uma reta numérica e represente as seguintes frações:

Questão 3
Janaína dividiu 1/5 do seu jardim para plantas hortaliças e 1/6 para fazer um jardim. Qual a fração total do seu quintal que será destinada a plantas?
(A) 11/30
(B) 1/11
(C) 5/6
(D) 2/11
Questão 4
Maria vai fazer um trabalho escolar e para isso precisa ler um livro com 500 páginas. Ela já leu 3/5 do livro, quantas páginas correspondem a essa quantidade?
(A) 300 páginas
(B) 200 páginas
(C) 250 páginas
(D) 350 páginas
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA07-A) Ler, entender, comparar e ordenar as frações associadas às ideias de inteiro e divisão, encontrado também as frações equivalentes, frações próprias, frações impróprias e frações aparentes, por meio da simplificação de frações. (EF06MA08-D) Representar os números racionais positivos na reta numérica utilizando a forma fracionária e a decimal e exemplos contextualizados, como pizza, tangram, recortes de papel. (EF06MA07-B) Associar uma fração imprópria a sua respectiva representação em forma de número misto. (EF06MA09) Ler, interpretar, resolver e elaborar problemas que envolvam o cálculo da fração de uma quantidade e cujo resultado seja um número natural, com e sem uso de calculadora. (EF06MA10) Ler, interpretar, resolver e elaborar problemas que envolvam adição ou subtração com números racionais positivos na representação fracionária. |
