Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 6° Período da Educação de Jovens e Adultos – EJA
Introdução
Duas retas paralelas cortadas por uma reta transversal, determinam vários tipos de ângulos que possuem nomes e relações específicas entre si. Este texto abordará esses diferentes ângulos formados, suas nomenclaturas e as propriedades que os relacionam.
Imagem do Autor produzida no Geogebra
Ângulos Correspondentes
Os ângulos correspondentes são aqueles que estão localizados do mesmo lado da transversal, um ângulo está dentro das retas paralelas e o outro está fora. Na imagem abaixo, o ângulo a é correspondente com o b e o ângulo c é correspondente com o d.
OBS. Existem outros.
Imagem do autor produzida no Geogebra
Propriedade
Se duas retas paralelas são cortadas por uma transversal, então cada par de ângulos correspondentes é congruente. Ou seja, possuem a mesma medida.
Na imagem, a é congruente com b e c é congruente com d.
Ângulos Alternos Internos e Externos
Os ângulos alternos internos são pares de ângulos que estão em lados opostos da transversal e dentro das duas retas paralelas, já os alternos externos estão, também em lados opostos, só que fora das duas retas paralelas. Veja na figura abaixo exemplos destes ângulos.
Imagem do autor produzida no Geogebra
Nas imagens, o ângulo o é alterno interno com o p e m é alterno interno do n. Já na outra imagem, o ângulo x é alterno externo do y e z é alterno externo do w.
Propriedade
Se duas retas paralelas são cortadas por uma transversal, então cada par de ângulos alternos internos e cada par de ângulos alternos externos é congruente. Ou seja, possuem a mesma medida.
Na imagem, m é congruente com n, o é congruente com p, x é congruente com y e z é congruente com w.
Ângulos Colaterais Internos e Externos
Os ângulos colaterais internos estão do mesmo lado da transversal e dentro das duas retas paralelas, já os colaterais externos, também estão do mesmo lado das duas paralelas, só que dentro das paralelas. Veja na figura abaixo exemplos destes ângulos.
Propriedade
Se duas retas paralelas são cortadas por uma transversal, então cada par de ângulos colaterais internos e cada par de ângulos colaterais externos são suplementares. Ou seja, a soma das medidas de cada par de ângulos é 1800.
Um exercício para finalizar
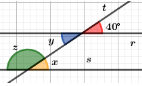
Determine a medida dos ângulos x, y e z, na imagem abaixo, sabendo que as retas r e s são paralelas e t uma transversal.
Imagem do autor produzida no Geogebra
Observando na figura temos:
- x é correspondente com 40º, logo x, também mede 40º.
- x é alterno interno com y, logo y, também mede 40º.
- z é colateral interno com y, logo z + y = 180°, como y = 40°, então z = 140º.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
Sabendo que as retas f e g são paralelas e que a reta h é uma transversal, calcule as medidas dos ângulos AGF, AGH, BGH, CHE, EHD e DHG na figura abaixo.
Arquivo pessoal do prof. Hélio
QUESTÃO 02
Observe a imagem abaixo, nela temos as retas paralelas (r e s), uma reta transversal (t) e alguns ângulos em destaque.
Fonte: Arquivo pessoal
Agora responda:
A) Quais ângulos são colaterais internos e externos?
B) Quais ângulos são alternos internos e externos?
C) Quais ângulos são correspondentes?
QUESTÃO 03
Sobre ângulos formados por retas paralelas cortadas por uma transversal, podemos afirmar que os
(A) colaterais externos são congruentes.
(B) correspondentes são complementares.
(C) colaterais são suplementares.
(D) alternos internos são suplementares.
QUESTÃO 04
Observe a figura.
Fonte: Arquivo pessoal
Nela podemos afirmar que soma das medidas dos ângulos EAD e ADI é igual a
(A) 135º.
(B) 180°.
(C) 90°.
(D) 360°.
SAIBA MAIS
Acesse o canal do prof. Hélio para aprender um pouco mais sobre ângulos formados por retas paralelas cortadas por uma transversal. Só clicar no vídeo.
| Autoria | Prof. Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EJAMA0616) Reconhecer relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6° ao 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6° ao 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. GOIÂNIA. Secretaria Municipal de Educação. Aprender Sempre. 6º ao 9º ano – Ensino Fundamental; Matemática; Goiânia, 2024. |
